Visuospatial Working Memory Development across Years of Schooling
Abstract
Background. Visuospatial working memory changes across years of schooling. According to data from the cross-sectional and longitudinal studies available in the literature, conclusions about the linear or nonlinear nature of changes in visuospatial working memory depend on the period of time analyzed and the frequency of the measurements. However, which of the two nonlinear models of functional dependence (e.g., quadratic or cubic) best describes the developmental trajectories of visuospatial memory across schooling is still an open question.
Objective. The results of statistical analysis of the development of visuospatial working memory in girls and boys across school years from Grade 1 to Grade 11 are presented. Additionally, the relationship between age and years of schooling is investigated, as is the influence of these factors on the developmental trajectory of visuospatial working memory.
Design. This cross-sectional study involved 1,246 pupils who were in Grades 1 to 11 at one public school; their ages ranged from 6.8 to 19.1 years (50.4% were boys). The students’ visuospatial working memory was measured using the computerized “Sequences” test, which is based on the “Corsi block-tapping task” and has been adapted for Russian schoolchildren. Correlations, dispersion analysis, and polynomial regression were carried out, and both linear and nonlinear models of the functional dependence of working memory on years of schooling were tested.
Results. The results of the multiple regression analysis suggest that number of years of schooling is a more important factor than age with regard to temporal changes in visuospatial working memory. When we introduced “years of schooling” and “age” predictors into a single model, we found the year of schooling to be the most significant predictor of visuospatial working memory (β = 1.07;p = 0.000).While age remained a statistically significant predictor (β = -0.52;p = 0.008), it did not significantly improve the model characteristics (corrected R2 = 0.30; F(2) = 253.9; p<0.01).
The results of the polynomial regression showed that during schooling, the developmental trajectories of visuospatial working memory are nonlinear for both genders. In girls, both the quadratic and cubic models explained 36% of the variance in visuospatial working memory, but the quadratic model had the least number of parameters and the best fit to data. In boys, despite all theoretical models being suitable, the largest percentage of the variance in visuospatial working memory values was explained using the cubic model (R2= 0.31; p = 0.000). Thus, the characteristic of change in visuospatial working memory for girls had a quadratic relationship that stabilized after Grade 8, while for boys, the relationship was cubic, with the period of stabilization between Grades 5 and 6, and then further growth.
Conclusion. We concluded that the number of years of study is an important factor in the development of visuospatial working memory during the schooling period, but that there are other factors involved as well.
Received: 17.07.2020
Accepted: 19.11.2020
Themes: Developmental psychology
PDF: http://psychologyinrussia.com/volumes/pdf/2020_4/Psychology_4_2020_207-222_Tikhomirova.pdf
Pages: 207-222
DOI: 10.11621/pir.2020.0414
Keywords: visuospatial working memory; school education; grade; age; cross-sectional study; polynomial regression; gender differences
Introduction
Working memory is the ability to temporarily store and process small pieces of information necessary for current thinking activities. According to one of the most developed concepts, working memory is a system consisting of a visuospatial matrix, a phonological loop, a central control element, and an episodic buffer that accumulates incoming information from different modalities (Baddeley & Hitch, 1994). In the context of educational problems, a special role in the working memory system is assigned to the visuospatial matrix, which is responsible for the storing and processing of spatial and visual information obtained in the process of direct perception or extracted from long-term memory (Tikhomirova & Malykh, 2017; Tikhomirova, 2017; Pagulayan et al., 2006, etc.).
Visuospatial working memory is measured by two types of tests. The first type measures static visuospatial working memory, which is related to the storage and reproduction of the spatial position of simultaneously presented stimuli (Roberts, 2016; Englund et al., 2014). The second type measures dynamic visuospatial working memory and consists of memorizing and reproducing sequentially represented stimuli (Pagulayan et al., 2006). This second type is often used to measure visuospatial working memory during school age, in particular, by the now-classic “Corsi block-tapping task” (Pagulayan et al., 2006). In this test, which has been adapted for Russian-speaking schoolchildren as “Sequences,” rows of blocks that light up in a certain order are presented on a computer screen, and then the test subject must repeat the order in which they lit up for each row (the rows consist of four to nine blocks) (Tikhomirova & Malykh, 2017; Tosto et al., 2013).
The phenomenon of working memory is often studied in cross-sectional studies of schoolchildren when there is a single measurement taken for children in different years of schooling, with different levels of education, etc. Longitudinal studies of working memory are much less frequently carried out. The essence of these is multiple measurements of a trait in the same respondents over a period of time, such as during the period of primary education, compulsory general education, etc. The choice of method is determined by the objectives of the study, the size of the samples, and the time and administrative capacities of the researcher (see in more detail Tikhomirova, Kuzmina, & Malykh, 2020). Thus, when using the data obtained at one point in time, the researcher is studying the specifics of change in a psychological trait over a certain period of time, such as, for example, the age features of each year of primary school education. The data collected in longitudinal studies make it possible to analyze the development of a trait over a certain period of time and to construct the trajectory of development during the whole schooling period.
Age and Years of Schooling in Changes in Visuospatial Working Memory
Both cross-sectional and longitudinal studies raise the problem of the relationship between student age and years of schooling, and their influence on the change in working memory. This problem is especially relevant for studies involving Russian schoolchildren and is associated with a wide range of age variability among children in each year of schooling. In one longitudinal study, the age differences between Russian students in first grade were as high as two years; and fourth-grade students’ average ages varied from 9.72 to 11.85 years (Tikhomirova et al., 2019). Additionally, there are significant overlaps in student age between different years of schooling. For example, a cross-sectional study involving Russian students from six general education schools showed that children aged 11 could be found studying in both the third grade and the fifth grade (Tikhomirova & Malykh, 2017). This can be due to a whole range of reasons, but it is primarily because parents can request early (at approximately 6.5 years) or late (closer to 8 years) entry of their child into the first grade.
The effects of student age and the number of years of study on cognitive skills were examined by Cahan & Cohen (1989) using a sample of peer children who entered school at different ages – usually a year early or a year late. They showed that students who entered the fifth grade a year earlier than their peers, performed better on intelligence tests by the end of the school year (Cahan & Cohen, 1989). Moreover, this performance gap remained until the end of the eighth year of schooling, indicating the significance of the effect that years of study have on cognitive skills development.
Another study compared the effects of age and learning activity in a sample of older people (Longman, Saklofske, & Fung, 2007). Statistically significant correlations between time spent on lifelong learning and average cognitive test scores were reported in older age groups. For example, the average IQ value among Americans with eight years of education is 86 or less, while that of their peers with sixteen years of educational experience is 112 (Longman, Saklofske, & Fung, 2007). However, in studies of the influence of student age and years of schooling on temporal changes in psychological traits, both measures are still equally considered and are sometimes used synonymously (Tikhomirova, Kuzmina, & Malykh, 2020; Kuzmina et al., 2020; Schneeweis, Skirbekk, & Winter-Ebmer, 2014; Isbell et al., 2015).
Changes in Visuospatial Working Memory across Lifespan
Working memory changes over time. This fact is observed in cross-sectional studies, which report an increase in average values (Tikhomirova et al., 2013; Roberts, 2016; Tikhomirova, 2017; Verbitskaya et al., 2015), and in longitudinal projects, which calculate trajectories of development over a certain time interval (López-Vicente et al., 2016; Isbell et al., 2015).
According to studies dating back 25 years, changes in working memory are nonlinear: working memory improves intensively while one is in primary and secondary school, and it declines in old age (Siegel, 1994). In particular, a study of working memory covering a broad age range from 5 to 80 years showed a significant increase in working memory during childhood, with only 30-year-old respondents reaching peak values (Alloway & Alloway, 2013). Thus, the change in this cognitive parameter appeared to be related to the specificity of the stimulus material in the working memory tests: verbal or visuospatial stimuli.
A study involving groups of respondents ages 6–10, 14–17, and 18–25 years showed that the cubic relationship between age and working memory test scores, with a stabilization period of 15–20 years, best describes changes in dynamic visuospatial memory (Roberts, 2016). However, this study had limitations due to the lack of data from respondents ages 11 to 13 years, and the small number of participants in each age group (approximately 100), which may have led to some distortion of the results. The hypothesis of the nonlinearity of the development of visuospatial working memory was also supported in a large-scale study with four repeated measurements over a one-year period in children ages 7–11 years (López-Vicente et al., 2016). The most intensive growth was recorded during the period from 7 to 10 years, while after 11 years of age, working memory had stabilized.
By contrast, a number of studies have reported linear changes in working memory from early childhood to adolescence (Isbell et al., 2015; Goldstein et al., 2014; Thaler et al., 2013). For example, a study of working memory based on the model by A. Baddley and G. Hitch analyzed the dynamics of individual components of working memory in children ages 4 to 15 years (Gathercole et al., 2004). It was shown that the trajectory of changes in working memory rose linearly from 4 to 14 years of age, stabilized at the ages of 14 to 15 years, and then plateaued. More recently, a study showed a similar trend in the nature of working memory change in a sample of children starting at 6 years old (Goldstein et al., 2014).
These studies also reported an earlier age-specific stabilization of working memory development at ages 11-12 years, but they still supported the conclusion of a linear pattern of change (Thaler et al., 2013). These studies also discussed the limitation of the upper-age range of samples, which is 14–15 years, leaving open the question of the further developmental trajectory of working memory, and acknowledging that stabilization in adolescence may be an indirect confirmation of the nonlinearity of the age dynamics of working memory. The thesis about the continued growth of working memory after stabilization in adolescence was proven in a study with three dimensions and children of 13, 16 and 20 years old (Isbell et al., 2015).
In studies involving Russian schoolchildren, it has been shown that at different stages of basic general education, there is an increase in average visuospatial working memory as measured by the “Sequences” test (Tikhomirova et al., 2013; Verbitskaya et al., 2015; Tikhomirova, 2017). It has been shown, in particular, that in primary school, the number of years of study explains 9% of the variation in visuospatial working memory values (Tikhomirova et al., 2015). It is emphasized that the increase in the average values of working memory test scores occurs at the expense of maximums. The minimums of working memory test scores actually remain unchanged during the period of primary school and during the basic level of general education (Tikhomirova& Malykh, 2017).
Thus, according to data from the cross-sectional and longitudinal studies available in the literature, conclusions about the linear or nonlinear nature of changes in visuospatial working memory depend on the period of time analyzed (up to 14, 25, or 80 years) and the frequency of measurements (only at 13, 16, and 20 years of age in the period from 13 to 20 years. or at 7, 8, 9, and 10 years of age in the period from 7 to 10 years). Which of the two nonlinear models of functional dependence (e.g., square or cubic) best describes the developmental trajectories of visuospatial memory is still an open question.
In this context, the most informative period is the period of school education, during which students actively master spatial activities, gain increased experience using computer technologies, and form geometric concepts. All of this promotes the intensive development of spatial abilities, including visuospatial working memory, making this cognitive trait plastic (Uttal et al., 2013; Jaušovec & Jaušovec, 2012). It is worth noting that boys’ greater interest in and experience with spatial activities are often used as an explanatory category when analyzing gender differences in spatial abilities (Frenken et al., 2016).
Gender differences in visuospatial working memory and their changes across lifespan
Gender differences in working memory are a common subject of cross-sectional studies that examine the periods of most intense growth and stabilization of mean working memory values in children, adolescents, youth, adults, and the elderly (Frenken et al., 2016). Several studies have reported the existence of gender differences in the development of visuospatialworking memory in favor of both men and women (León, Cimadevilla,& Tascón, 2014; Bull, Davidson, &Nordmann, 2010; Wai, Lubinski, &Benbow, 2009; Voyer et al, 2007; Vuontela et al., 2003, etc.).Other studies have demonstrated similarities in the age dynamics of working memory test scores that include visuospatial stimuli (e.g., Robert & Savoie, 2006).
It has been shown that in the period from 6 to 13 years of age, gender differences in performance on visuospatial working memory tests are most evident at6 to 8 years of age, less evident at 9 to 10 years of age, and absent at 11 to 13 years of age (Vuontela et al., 2003). Throughout the analyzed age period, girls performed tasks better than boys with fewer errors. A slightly different result was obtained in the meta-analysis of 36 studies that included the following age groups:under 13, 13 to 18, and over 18 years of age (Voyer et al., 2007). For example, significant gender differences, favoring women, were found in age groups older than 13 years.
However, most studies have reported a male advantage in performance on visuospatial working memory tests (e.g., Tikhomirova et al., 2015; Zilles et al., 2016; Frenken et al., 2016; Bull, Davidson, & Nordmann, 2010; Wai, Lubinski, &Benbow, 2009). For example, a statistically significant effect of the influence of gender, favoring boys, was obtained in samples of Russian high school students (Tikhomirova et al., 2013) and primary school students (Tikhomirova et al., 2015).
However, the advantage of each gender during the performance of visuospatial working memory tests can be related to the dynamics of change at certain age stages. For example, in a longitudinal study of gender differences in working memory developmental trajectories, seven-year-old girls performed worse than their male peers, but during the course of the year, girls experienced more intensive growth, which resulted in higher visuospatial memory scores for girls at eight years of age (López-Vicente et al., 2016). The fact that there are gender differences in working memory, as with most cognitive traits, is explained in the context of biological (Zilles et al., 2016) and sociocultural (Frenken et al., 2016) paradigms.
Thus, the results of studies on gender differences in the developmental trajectory of visuospatial working memory show different and sometimes diametrically opposite results, which are due, among other things, to the shortness of the time intervals during which the working memory is analyzed (in particular, younger schoolchildren and adolescents ages 6–13 years or only younger schoolchildren ages 7–11 years). Analyzing this psychological trait over a longer period of time, and covering different age periods, will make it possible to identify periods of growth, assess their intensity, and determine the stages of stabilization of the trait in both genders.
The Current Study
The current cross-sectional study aimed to analyze changes in visuospatial working memory in girls and boys throughout the whole schooling period, with measurements during each year – from the first to the eleventh grade. Expanding the period of schooling to include early school age, adolescence, and youth, increases the likelihood of understanding the influence of gender on changes in visuospatial working memory. In addition, this study investigated the problem of the relationship between student age and year of schooling, and analyzed their effects on temporal changes in working memory.
Methods
Participants
Our study involved 1,246 pupils in Grades 1–11 at one school; the pupils were ages 6.8 to 19.1 years (50.4% boys). There were 501 students in the primary school-age sample (Grades 1–4, primary level of general education; average age = 9.23 years; standard deviation = 1.12; 49.9% boys); 542 students in the secondary school-age sample (Grades 5–9, basic level; average age = 14.06 years; standard deviation = 1.56; 54.8% boys); and 203 students in the high school-age sample (Grades 10–11, full general education; mean age = 17.25 years; standard deviation = 0.68; 39.9% boys).
Table 1 provides a detailed description of the sample according to year of schooling (first to eleventh grades).
Procedure
To measure visuospatial working memory, we used the computerized “Sequences” test based on the “Corsi block-tapping task” (Pagulayan et al., 2006) adapted from studies involving Russian and British schoolchildren (Tikhomirova & Malykh, 2017; Tikhomirova, 2017; Tosto et al., 2013).
During the first stage of the tests, sets of blocks appear on the computer screen and light up one after another in a certain order; blocks light up in yellow for one second at intervals of one second. During the second stage, the “Start”command appears on the screen, and the participant must use the computer mouse to click on the blocks in the same order in which they lit up during the first stage.
The test begins with the test participant being presented with two sets (sequences) of 4 blocks. If the test participant fails to repeat both accurately, the test is automatically terminated. If the test participant repeats at least one of the sequences correctly, a sequence of increased difficulty is presented, with the number of blocks increased by one. The maximum number of blocks in a sequence is equal to 9.The test program records the number of correctly repeated sequences.
Written informed consent of parents and school administration representatives was obtained for the participation of schoolchildren. The study was approved by the Ethics Committee of the Psychological Institute of the Russian Academy of Education (project identification code 2016/2–12). The data analysis was carried out on the basis of anonymized personal data.
Data collection was carried out in the computer science class strictly according to the developed protocols and under the supervision of the researcher. Each study participant executed the ”Sequences“ test on a personal computer with a 17-inch monitor, at a distance of 60 cm from the screen. More detailed information about the sample and procedure are available at Tikhomirova, Malykh, & Malykh, 2020; Verbitskaya et al., 2020.
Statistical Approach
At the first stage, the age variability of the participants in each year of schooling was analyzed. The correlation analysis between student age and years of schooling was carried out, and multiple regression analysis was conducted to determine the indicator of working memory, where the student age and year of schooling variables were used as predictors. Multiple regression allows the measurement of the contribution of student age and number of years of study to be included in the dispersion of the visuospatial working memory values.
At the second stage, descriptive visuospatial working memory statistics for girls and boys were calculated for each year of schooling. To assess the statistical significance of gender differences and measure the effect of gender on working memory in each year of schooling, a one-factor dispersion analysis was performed.
At the third stage, correlation analysis was carried out for samples of both genders in order to assess the relationship between year of schooling and visuospatial working memory.
During the fourth stage, polynomial regression was used to analyze age-related changes in visuospatial working memory; this allowed the testing of both linear and nonlinear (in particular, square and cubic) models of the functional dependence of the analyzed feature. Polynomial regression was performed on a general sample, as well as on groups of girls and boys, to analyze gender differences in working memory changes during schooling. The least squares method was used to estimate the parameters of the regression equation.
Results and Discussion
Age and Year of Schooling, their Relationship, and the Effects on Working Memory Development
Table 1 shows age, gender, and sample sizes for each year of schooling.
Table 1
Description of Sample
|
Level of school education |
Year of schooling |
N |
Average age (min – max) |
Nboys (%) |
|
Elementary |
1 |
146 |
7.86 (6.8 – 7.8) |
51.4 |
|
2 |
117 |
8.85 (7.8 – 9.5) |
49.6 |
|
|
3 |
140 |
9.82 (8.8 – 10.9) |
50.7 |
|
|
4 |
98 |
10.85 (10.0 – 11.6) |
46.9 |
|
|
Secondary |
5 |
102 |
11.81 (10.8 – 13.0) |
63.7 |
|
6 |
98 |
12.81 (11.7 – 14.1) |
59.2 |
|
|
7 |
69 |
13.78 (12.8 – 15.1) |
53.6 |
|
|
8 |
101 |
14.81 (13.6 – 16.1) |
59.4 |
|
|
9 |
172 |
15.77 (14.2 – 18.0) |
44.8 |
|
|
High |
10 |
100 |
16.72 (15.3 – 17.0) |
35.0 |
|
11 |
103 |
17.77 (16.3 – 19.1) |
44.7 |
|
|
Total |
1 – 11 |
1246 |
12.64 (6.8 – 19.1) |
50.4 |
As shown in Table 1, the average student age increases by one year every year– from 7.86 years in the first grade, to 17.77 in the eleventh grade. Thus, the difference in average age values from grade to grade is one year. Additionally, the wide range of age variability within one year of schooling warrants attention. For example, the difference in age between students in the sixth grade is almost three years, with a minimum of 11.7 years and a maximum of 14.1 years. In the ninth grade, the difference can be even greater: the average age is 15.77 years, but both 14-year-olds and 18-year-olds can be studying in the same grade. This wide variation is due to a number of reasons but primarily to the child’s early or late entry into first grade at the request of parents (from 6.5 or 8.0 years of age), the need to reeducate a child with poor academic performance to repeat a grade, or health problems, etc.
In addition, there are significant overlaps in ages between different years of schooling. For example, according to Table 1, a child aged 13 can be enrolled in the fifth,sixth, or seventh grade. Nevertheless, both student age and year of schooling can be simultaneously considered as predictors when analyzing changes in visuospatial working memory (Tikhomirova, Kuzmina, & Malykh, 2020; Kuzmina et al., 2020; Isbell et al., 2015).
The results of the correlation analysis between schoolchildren’s age and years of schooling showed a very high correlation (r = 0.993; p<0.01). However, despite this high correlation coefficient, each of these factors may have a unique effect on cognitive development (see, for example, Schneeweis, Skirbekk, & Winter-Ebmer, 2014).
The multiple regression analysis, where age and year variables were used as predictors, allowed us to measure the contribution of each of these variables to the variation of visuospatial working memory. Thus, with the help of the “years of schooling” predictor, 30% of the dispersion of the working memory index was explained (model characteristics: corrected R2= 0.30; F = 498.2; p<0.01), while with the help of the “age” predictor, only 28% was explained (model characteristics: corrected R2= 0.28; F = 467.5; p<0.01). When the variables were introduced into one regression model, years of schooling were determined to be the most significant predictor of visuospatial memory (β = 1.07 at p= 0.000), while age, which remained a statistically significant predictor (β = -0.52 at p= 0.008), did not significantly improve the model characteristics (corrected R2= 0.30; F(2) = 253.9; p<0.01).
This result suggests that number of years of study is a more important factor than age in changes in visuospatial memory, and this result is consistent with those from studies on the impact of education on cognitive development (Schneeweis, Skirbekk, & Winter-Ebmer, 2014; Nisbett et al., 2012; Longman, Saklofske, & Fung, 2007, etc.).
Further analysis will examine changes in visuospatial working memory in relation to years of schooling from the first grade to the eleventh grade.
Visuospatial Working Memory: Changes across Schooling
Table 2presents the average, minimum, and maximum scores of visuospatial working memory for girls and boys in each year of schooling.
Table 2
Descriptive statistics of visuospatial working memory
|
Level of school education |
Year of schooling |
Girls |
Boys |
|
Elementary |
1 |
1.09 (0 – 5) |
1.09 (0 – 5) |
|
2 |
1.85 (0 – 5) |
1.77 (0 – 5) |
|
|
3 |
2.10 (0 – 6) |
3.04 (0 – 7) |
|
|
4 |
2.75 (0 – 7) |
3.87 (0 – 7) |
|
|
Secondary |
5 |
2.70 (0 – 6) |
3.82 (0 – 8) |
|
6 |
3.97 (0 – 8) |
3.84 (0 – 7) |
|
|
7 |
4.57 (0 – 9) |
4.28 (0 – 9) |
|
|
8 |
5.10 (2 – 9) |
4.79 (0 – 10) |
|
|
9 |
4.91 (0 – 9) |
4.99 (0 – 11) |
|
|
High |
10 |
5.01 (0 – 8) |
5.09 (0 – 9) |
|
11 |
5.10 (0 – 8) |
5.20 (0 – 10) |
|
|
Total |
1 – 11 |
3.39 (0 – 9) |
3.59 (0 – 11) |
Table 2presents the average values for the number of correct answers for the “Sequences” test, as well as minimums and maximums (in brackets) of the working memory index for girls and boys in each year of school education. The minimum and maximum values for the sequences test are 0 and 12, respectively.
According to Table 2, the dynamics of visuospatial memory growth are different for boys and girls during schooling, even as they have same starting values in the first grade (1.09). Boys have more intensive growth from the second to fourth years of schooling, while girls have more intensive growth from the fifth to eighth years. However, by the end of basic general education (ninth grade) and full general education (eleventh grade), the rates of growth for both genders are almost identical (for example, 4.91 for girls and 4.99 for boys in the ninth grade).
The analysis of variance reveals statistically significant gender differences in working memory only in the third (effect size of 9% of variance), fourth (10%), and fifth (5%) years of schooling (p<0.01). The best performance on the “Sequences” test was observed in boys in the third to fifth years of schooling (see average values in Table 2). These results are fully consistent with the available literature on the male advantage in spatial abilities, including visuospatial working memory (Tikhomirova, 2017; Frenken et al., 2016; Bull, Davidson, & Nordmann, 2010; Wai, Lubinski, & Benbow, 2009).
According to the result of the analysis of variance, interaction between sex and year of schooling in the total sample was statistically significant (p<0.05), indicating that there are the differences in visuospatial working memory between boys and girls across all schooling.
Results of the analysis of working memory in boys and girls showed that, in general, boys demonstrate a wider range of scores – from 0 to 11 of the maximum possible 12 points on the sequences test. This fact is often used as an explanation for the existence of gender differences in spatial abilities and the gender gap in high-tech industries that favor men (Wai, Lubinski, &Benbow, 2009; Zilles et al., 2016).
Correlation analysis between the years of schoolingand working memory test scores was performed on the total sample, and in samples of boys and girls. The results showed the Spearman's correlation coefficient for the total sample of schoolchildren to be 0.55 (p<0.01), indicating a noticeable relationship between year of schooling and visuospatial working memory. Additionally, gender differences in these relationships were found. Thus, a slightly higher correlation coefficient (r = 0.60 at p<0.01) was obtained in a sample of girls compared to boys (r = 0.51 at p<0.01), which points to differences in their patterns of the development of working memory during the schooling period.
According to several studies, the development of working memory is characterized by intensive growth in the period from 6 to 14 years of age (according to Thaler et al. [2013], up to 11 – 12 years old), stabilization at the age of 11 – 15 years (Goldstein et al., 2014), and another period of growth with a peak at 30 years (Isbell et al., 2015; Alloway & Alloway, 2013). In other words, throughout the entire period of schooling – from 6.5 to 19 years of age – the development of visuospatial working memory follows a nonlinear trajectory.
Polynomial regression was used to determine the linearity or nonlinearity of the development of visuospatial working memory. In the course of analysis, both linear and nonlinear (in particular, square and cubic) models of functional dependence of working memory on the school year were tested.
Table 3presents the results of the polynomial regression analysis, where the number of correct responses on the “Sequences” in the visuospatial working memory test was used as a dependent variable. In the course of the analysis, linear, square, and cubic dependencies of the working memory on the year of schooling were estimated.
Polynomial regression was carried out sequentially on the general sample of all schoolchildren (T), on the sample of girls (F), and on the sample of boys (M). The method of least squares was used to estimate the parameters of the regression equation.
Table 3
Results of polynomial regression on visuospatial working memory test scores
|
Relationship |
Model Summary |
Parameter Estimates |
||||||||
|
R2 |
F |
df1 |
df2 |
p |
Const. |
b1 |
b2 |
b3 |
||
|
Linear |
T |
0.29 |
498.3 |
1 |
1168 |
0.000 |
1.030 |
0.39 |
|
|
|
|
F |
0.34 |
307.4 |
1 |
578 |
0.000 |
1.024 |
0.39 |
|
|
|
|
M |
0.25 |
205.7 |
1 |
588 |
0.000 |
1.500 |
0.37 |
|
|
|
Quadratic |
T |
0.32 |
277.9 |
2 |
1167 |
0.000 |
0.294 |
0.86 |
-0.04 |
|
|
|
F |
0.36 |
164.4 |
2 |
577 |
0.000 |
0.228 |
0.79 |
-0.03 |
|
|
|
M |
0.29 |
119.8 |
2 |
587 |
0.000 |
0.392 |
0.90 |
-0.05 |
|
|
Cubic |
T |
0.32 |
185.2 |
3 |
1166 |
0.000 |
0.210 |
0.93 |
-0.06 |
0.01 |
|
|
F |
0.36 |
110.8 |
3 |
576 |
0.000 |
0.732 |
0.37 |
0.05 |
-0.01 |
|
|
M |
0.31 |
81.5 |
3 |
586 |
0.000 |
-0.253 |
1.45 |
-0.16 |
0.01 |
According to Table 3, all analyzed theoretical models – linear, square, and cubic – fit the empirical data well for the general sample of schoolchildren. The linear model showed directly proportional growth of visuospatial working memory during school education and explained 29% of the variation of this cognitive index (p = 0.000). The higher percentage of dispersion in the working memory test scores was explained by using nonlinear models: R2 for both square and cubic dependencies was 0.32 at p= 0.000. However, the quadratic model had a smaller number of parameters, which to some extent indicated better correspondence with the empirical data.
In the sample of girls, all of the analyzed theoretical models also fit the empirical data well. Thus, 34% of the dispersion in the working memory test scores was explained using a linear model (p = 0.000). A larger percentage of the dispersion in the analyzed variable was explained in the framework of nonlinear models – quadratic and cubic (for both models R2= 0.36 at p = 0.000). However, when comparing the number of parameters, the quadratic dependence model better described the data.
In the sample of boys, despite all theoretical models being suitable, the largest percentage of dispersion of working memory values was explained using the cubic model (R2= 0.31 at p = 0.000). Twenty-five percent and 29% of the dispersion of working memory in boys was explained in terms of the linear and quadratic models, respectively.
Thus, during the period of schooling for both girls and boys, the change in visuospatial working memory was nonlinear. However, the change in working memory in girls was best described with a quadratic relationship, and in boys, it was best described with a cubic relationship. To be more precise, for girls, a gradual increase in the average values of working memory from the first to the fifth year of school was observed, followed by more intensive growth from the fifth to eighth grades and from the eighth to eleventh years, with stabilization occurring with a slight decrease in grades 9-10. This trajectory was best described by a graph of quadratic function—a parabola.
Boys of school age presented a different picture with regard to changes in working memory. According to the results of the analysis, working memory improved intensely from the second to the fourth year of schooling; in the 5th to 6th grades, the growth stabilized; and from the seventh to the eleventh year, working memory improved again, but this improvement was not as intense as it was at the beginning of the schooling period. This pattern of change fit the cubic parabola well. The identified gender differences in the developmental trajectories of visuospatial working memory are presented in Figure 1(1a for girls and 1b for boys).
In Figure 1, the X-axis corresponds to the school year – from the first to eleventh grade (1 – 11); the Y-axis corresponds to the number of correct answers on the “Sequences” test (0 – 12). The linear function is indicated with a solid line, the quadratic function is indicated with a dashed line, and the cubic function is indicated with a dash-dot line.
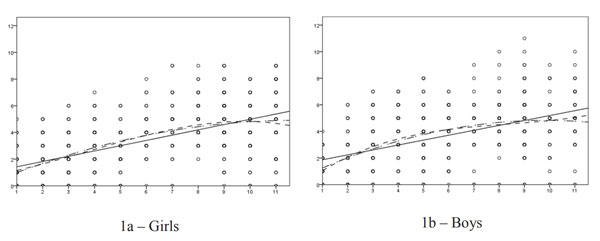
Figure 1. Dependence of visuospatial working memory on years of schooling
As seen in Figure 1, the graphs of the quadratic function for girls and the cubic function in boys describe the observed measures of visuospatial working memory more accurately than the linear graphs. Confirmation of the nonlinearity of the development of working memory throughout the entire period of schooling observed in this study aligns with the data on the pronounced cubic relationship between student age and test scores on the spatial memory sequences test in the period from 5 to 25 years (Roberts, 2016).
A study which set the upper limit of the age range of respondents of both genders at 14 years reported a linear improvement in working memory up to 11-12 years and further stabilization (Goldstein et al., 2014; Thaler et al., 2013). This result points to nonlinear dynamics in working memory development. These data are fully consistent with the results obtained in this study with the sample of boys: intensive growth with stabilization in the 5th and 6thgrades (this corresponds to the ages of 11 – 12 years), and improvement in working memory from the 7th to 11th grades (ages 13.8 to 17.8 years).
Different results were observed in the girls’ sample, with improvement in working memory observed up to the 8th grade (average age 14.8 years), and then stabilization that continued until the 11th grade (14.8 to 17.8 years old). These results echo the results of a study of the trajectories of the development of working memory in children up to the age of 15, which reported stabilization in boys and girls ages 14–15 years (Gathercole et al., 2004). The specifics of the development of visuospatial working memory in girls and boys presented in this work can to some extent explain the differences reported by existing studies, with regard to the beginning of the stabilization period in samples that included both genders (Goldstein et al., 2014; Thaler et al., 2013; Gathercole et al., 2004).
The results of polynomial regression on the sample of girls, using the number of years of schooling, found a slightly larger percentage of the dispersion of visuospatial working memory compared to that observed for boys. Thus, in the framework of both linear and nonlinear models for girls, the multiple determination coefficient R2varied between 0.34 and 0.36, while in boys it was between 0.25 and 0.31 (p = 0.000). These data confirm a stronger dependence of the development of working memory on years of schooling in girls than in boys, confirming the data on the relationship between behavioral level and gender specificity with regard to neurophysiological maturation, including differences in the degree of right-hand activation of Broca's zone (Zilles et al., 2016).
Conclusion
In this cross-sectional study, we studied the development of visuospatial working memory of girls and boys throughout their whole schooling period, taking measurements during each year from the first to eleventh grades.
A large sample of 1246 schoolchildren, ages 6.8 to 19.1 years, showed a wide range of student age variability within one year of schooling – the age difference among students of the same grade could be up to three years. Significant overlaps in student age between different years of schooling were also observed; for example, children aged 13 years could be studying in the fifth grade or in the sixth or even seventh grade. This made the study of the relationship between student age and year of schooling and their effects on the development of working memory particularly relevant.
Despite the high correlation between age and number of years of schooling, each of these indicators had a unique effect on cognitive development. Indeed, the results of the multiple regression analysis, in which the variables of age and year of schooling were used as predictors, indicated that the number of years of study was a more significant factor than age in the development of visuospatial working memory.
Polynomial regression showed that changes in visuospatial working memory are nonlinear during schooling for both girls and boys. The nature of change in working memory in girls resembled a quadratic relationship, with intensive growth from the fifth to the eighth year of education that stabilized after the eighth grade, whereas in boys, it resembled a cubic relationship, with intensive growth in the period from the second to the fourth year of education, stabilization between the fifth and sixth years, and then further growth.
According to the results of polynomial regression, 29 to 32% of the variation in visuospatial working memory was explained in the total sample of schoolchildren within the framework of linear and nonlinear regression. This result suggests that years of schooling, despite being important in the development of working memory during the schooling period, are not the only factor that affects the development of visuospatial working memory.
Limitations
This study has a number of strengths, including well-validated measurement of visuospatial working memory in a relatively large sample (N > 1,200). At the same time, the study has limitations since it omitted important factors (such as the SES of participants’ families), which can affect the results. Unfortunately, these characteristics are not available for this sample and cannot be used in analysis.
Further directions for research include longitudinal studies, which could make it possible to understand the age-related factors that influence changes in visuospatial working memory, and to calculate the individual trajectories of the development of this cognitive trait in both boys and girls during the whole schooling period.
Acknowledgements
This research was supported by a grant (No. 17-78-30028) from the Russian Science Foundation.
References
Alloway, T.P., & Alloway, R.G. (2013). Working memory across the lifespan: A cross-sectional approach. Journal of Cognitive Psychology, 25(1), 84-93. https://doi.org/10.1080/20445911.2012.748027
Baddeley, A.D., & Hitch, G.J. (1994). Developments in the concept of working memory. Neuropsychology, 8(4), 485. https://doi.org/10.1037/0894-4105.8.4.485
Bull, R., Davidson, W.A., & Nordmann, E. (2010). Prenatal testosterone, visuospatial memory, and numerical skills in young children. Learning and Individual Differences, 20(3), 246-250.https://doi.org/10.1016/j.lindif.2009.12.002
Cahan, S., & Cohen, N. (1989). Age versus schooling effects on intelligence development. Child Development, 1239-1249. https://doi.org/10.2307/1130797
Englund, J.A., Decker, S.L., Woodlief, D.T., & DiStefano, C. (2014). Development and evaluation of an online, multicomponent working memory battery. Assessment, 21(5), 543-561.https://doi.org/10.1177/1073191114524016
Frenken, H., Papageorgiou, K.A., Tikhomirova, T., Malykh, S., Tosto, M.G., & Kovas, Y. (2016). Siblings' sex is linked to mental rotation performance in males but not females. Intelligence, 55, 38-43. https://doi.org/10.1016/j.intell.2016.01.005
Gathercole, S.E., Pickering, S.J., Ambridge, B., & Wearing, H. (2004). The structure of working memory from 4 to 15 years of age. Developmental Psychology, 40(2), 177-190. https://doi.org/10.1037/0012-1649.40.2.177
Goldstein, G., Allen, D.N., Thaler, N.S., Luther, J.F., Panchalingam, K., & Pettegrew, J.W. (2014). Developmental aspects and neurobiological correlates of working and associative memory. Neuropsychology, 28(4), 496-505. https://doi.org/10.1037/neu0000053
Isbell, E., Fukuda, K., Neville, H.J., & Vogel, E.K. (2015). Visual working memory continues to develop through adolescence. Frontiers in Psychology, 6, 696. https://doi.org/10.3389/fpsyg.2015.00696
Jaušovec, N., & Jaušovec, K. (2012). Sex differences in mental rotation and cortical activation patterns: Can training change them? Intelligence, 40(2), 151-162. https://doi.org/10.1016/j.intell.2012.01.005
Kuzmina, Y., Tikhomirova, T., Lysenkova, I., & Malykh, S. (2020). Domain-general cognitive functions fully explained growth in nonsymbolic magnitude representation but not in symbolic representation in elementary school children. PloS one, 15(2), e0228960. https://doi.org/10.1371/journal.pone.0228960
León, I., Cimadevilla, J.M., & Tascón, L. (2014). Developmental gender differences in children in a virtual spatial memory task. Neuropsychology, 28(4), 485. https://doi.org/10.1037/neu0000054
Longman, R.S., Saklofske, D.H., & Fung, T.S. (2007). WAIS-III percentile scores by education and sex for US and Canadian populations. Assessment, 14(4), 426-432. https://doi.org/10.1177/1073191107304114
López-Vicente, M., Forns, J., Suades-González, E., Esnaola, M., García-Esteban, R., Álvarez-Pedrerol, M., ... Sunyer, J. (2016). Developmental trajectories in primary schoolchildren using n-back task. Frontiers in Psychology, 7, 716. https://doi.org/10.3389/fpsyg.2016.00716
Nisbett, R.E., Aronson, J., Blair, C., Dickens, W., Flynn, J., Halpern, D.F., & Turkheimer, E. (2012). Intelligence: new findings and theoretical developments. American Psychologist, 67(2), 130-159. https://doi.org/10.1037/a0026699
Pagulayan, K., Busch, R.M., Medina, K.L., Bartok, J.A., & Krikorian, R. (2006). Developmental normative data for the Corsi Block-tapping task. Journal of Clinical and Experimental Neuropsychology, 28(6), 1043-1052. https://doi.org/10.1080/13803390500350977
Robert, M., & Savoie, N. (2006). Are there gender differences in verbal and visuospatial working-memory resources? European Journal of Cognitive Psychology, 18(03), 378-397. https://doi.org/10.1080/09541440500234104
Roberts, K.L. (2016). Developmental Trajectories of Working Memory from Age 6 through 25 Years. Retrieved from https://scholarcommons.sc.edu/etd/3512/
Schneeweis, N., Skirbekk, V., & Winter-Ebmer, R. (2014). Does education improve cognitive performance four decades after school completion? Demography, 51(2), 619-643. https://doi.org/10.1007/s13524-014-0281-1
Siegel, L.S. (1994). Working memory and reading: A life-span perspective. International Journal of Behavioral Development, 17(1), 109-124. https://doi.org/10.1177/016502549401700107
Thaler, N.S., Goldstein, G., Pettegrew, J.W., Luther, J.F., Reynolds, C.R., & Allen, D.N. (2013). Developmental aspects of working and associative memory. Archives of Clinical Neuropsychology, 28(4), 348-355. https://doi.org/10.1093/arclin/acs114
Tikhomirova, T.N., Malykh, S.B., Bogomaz, S.A., Sudneva, O.V., &Kovas, Y.V. (2013). Prostranstvennoe myshlenie i pamyat' u starsheklassnikov s razlichnym urovnem matematicheskoj beglosti [Spatial thinking and memory in high school students with different levels of mathematical fluency]. Teoreticheskaya i eksperimental'naya psihologiya [Theoretical and Experimental Psychology], 6(4), 99-109.
Tikhomirova, T.N., Modyaev, A.D., Leonova, N.M., &Malykh, S.B. (2015). Faktory uspeshnosti v obuchenii nanachal’noj stupeni obshchego obrazovaniya: polovyerazlichiya [Factors of academic achievementat primary school level: sex differences]. Psihologicheskij Zhurnal [Psychological Journal], 36(5), 43-54.
Tikhomirova, T.N., Kuzmina, Y.V., & Malykh, S.B. (2020). Traektorii razvitiya skorosti pererabotki informacii v mladshem shkol'nom vozraste: longityudnoe issledovanie [Trajectories of processing speed development across primary school years: longitudinal study]. Psihologicheskij Zhurnal [Psychological Journal],41(2), 26-38. https://doi.org/10.31857/S020595920008507-3
Tikhomirova, T. (2017). Spatial thinking and memory in Russian high school students with different levels of mathematical fluency. Procedia - Social and Behavioral Sciences, 237, 1260-1264.https://doi.org/10.1016/j.sbspro.2017.02.204
Tikhomirova, T.N., &Malykh, S.B. (2017). Kognitivnye osnovy individual'nyh razlichij v uspeshnosti obucheniya [Cognitive bases of individual differences in academic achievement]. M.; SPb.: Nestor-History.
Tikhomirova, T., Kuzmina, Y., Lysenkova, I., & Malykh, S. (2019). Development of approximate number sense across the elementary school years: A cross-cultural longitudinal study. Developmental Science, 22(4), e12823. https://doi.org/10.1111/desc.12823
Tikhomirova, T., Malykh, A., & Malykh, S. (2020). Predicting Academic Achievement with Cognitive Abilities: Cross-Sectional Study across School Education. Behavioral Sciences, 10(10), 158. https://doi.org/10.3390/bs10100158
Tosto, M.G., Tikhomirova, T., Galajinsky, E., Akimova, K., & Kovas, Y. (2013). Development and Validation of a Mathematics-number sense Web-based Test Battery. Procedia - Social and Behavioral Sciences, 86, 423-428.https://doi.org/10.1016/j.sbspro.2013.08.591
Verbitskaya, L.A., Malykh, S.B., Zinchenko, Y.P., & Tikhomirova, T.N. (2015). Cognitive predictors of success in learning Russian. Psychology in Russia. State of the Art, 8(4), 91-100. https://doi.org/10.11621/pir.2015.0408
Verbitskaya, L.A., Zinchenko, Y.P., Malykh, S.B., Gaidamashko, I.V., Kalmyk, O. A., & Tikhomirova, T.N. (2020). Cognitive Predictors of Success in Learning Russian Among Native Speakers of High School Age in Different Educational Systems. Psychology in Russia. State of the Art, 13(2), 2-15. https://doi.org/10.11621/pir.2020.0201
Voyer, D., Postma, A., Brake, B., & Imperato-McGinley, J. (2007). Gender differences in object location memory: A meta-analysis. Psychonomic bulletin & review, 14(1), 23-38. https://doi.org/10.3758/BF03194024
Vuontela, V., Steenari, M.R., Carlson, S., Koivisto, J., Fjällberg, M., & Aronen, E. T. (2003). Audiospatial and visuospatial working memory in 6–13 year old school children. Learning & Memory, 10(1), 74-81. https://doi.org/10.1101/lm.53503
Wai, J., Lubinski, D., & Benbow, C.P. (2009). Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. Journal of Educational Psychology, 101(4), 817.https://doi.org/10.1037/a0016127
Zilles, D., Lewandowski, M., Vieker, H., Henseler, I., Diekhof, E., Melcher, T., ... Gruber, O. (2016). Gender differences in verbal and visuospatial working memory performance and networks. Neuropsychobiology, 73(1), 52-63. https://doi.org/10.1159/000443174
To cite this article: Tikhomirova, T.N., Malykh, A.S., Malykh, S.B. (2020). Visuospatial Working Memory Development across Years of Schooling. Psychology in Russia: State of the Art, 13(4), 207-222.
The journal content is licensed with CC BY-NC “Attribution-NonCommercial” Creative Commons license.










