The concentric model of human working memory: A validation study using complex span and updating tasks
Abstract
Background. Working memory (WM) seems to be central to most forms of high-level cognition. This fact is fueling the growing interest in studying its structure and functional organization. The influential “concentric model” (Oberauer, 2002) suggests that WM contains a processing component and two storage components with different capacity limitations and sensitivity to interference. There is, to date, only limited support for the concentric model in the research literature, and it is limited to a number of specially designed tasks.
Objective. In the present paper, we attempted to validate the concentric model by testing its major predictions using complex span and updating tasks in a number of experimental paradigms.
Method. The model predictions were tested with the help of review of data obtained primarily in our own experiments in several research domains, including Sternberg’s additive factors method; factor structure of WM; serial position effects in WM; and WM performance in a sample with episodic long-term memory deficits.
Results. Predictions generated by the concentric model were shown to hold in all these domains. In addition, several new properties of WM were identified. In particular, we recently found that WM indeed contains a processing component which functions independent of storage components. In turn, the latter were found to form a storage hierarchy which balances fast access to selected items, with the storing of large amounts of potentially relevant information. Processing and storage in WM were found to be dependent on shared cognitive resources which are dynamically allocated between WM components according to actual task requirements. e implications of these findings for the theory of WM are discussed.
Conclusion. The concentric model was shown to be valid with respect to standard WM tasks. The concentric model others promising research perspectives for the study of higher- order cognition, including underlying neurobiological mechanisms.
Received: 19.03.2016
Accepted: 29.08.2016
Themes: Cognitive psychology
PDF: http://psychologyinrussia.com/volumes/pdf/2017_3/psych_3_2017_6.pdf
Pages: 74-92
DOI: 10.11621/pir.2017.0305
Keywords: working memory, concentric model, focus of attention (FA), storage, processing, interference, long-term memory (LTM), serial position e ects, complex span task, updating task
Introduction
Working memory (WM) is a central component in many theories of cognition. It is a system for on-line storage and processing of information serving the completion of an actual task (Baddeley, 2012). There has been an explosion of research interest in WM over the last decades. This is surely driven by its theoretical prominence, but even more by significant practical links between WM and higher-level cognition. WM has been shown to be strongly related to fluid intelligence (Ackerman et al., 2005), and to the effectiveness of complex activities like foreign language learning, understanding instructions, and control of technical systems (Engle, 2002). WM is also related to academic achievement, and its deficit may be a major cause of learning deficits in school-age children (Gathercole & Alloway, 2008). The proper understanding of WM mechanisms may thus have important practical applications.
The research on the structure and function of WM has long been dominated by Baddeley’s multi-component model (Baddeley, 1986). However, studies of individual differences in the limits of WM capacity (Daneman & Carpenter, 1980; Turner & Engle, 1989; Engle, 2002; Shipstead, Harrison, & Engle,2016) shed a different light on this problem. First, these studies showed a close link between WM capacity and controlled attention. Second, they questioned the fundamental distinction between WM, usually associated with short-term memory (STM), and long-term memory (LTM), suggesting that WM is comprisedof elements activated in the LTM. For instance, in the embedded processes theory (Cowan, 1999), a three-layer organization of memory is suggested. The basic layer is formed by the unlimited LTM, from which is selected a subset of activated representation (activated LTM=a-LTM), from which in turn emerges a very limited subset of representations in the focus of attention (FA). Information in the FA can be manipulated and is immune to interference and decay, contrary to that in the a-LTM. Components of WM are characterized by different states of activation–a discovery which gave rise to the notion of activation models of WM.
The most elaborated example of such models is the concentric model by K. Oberauer (Oberauer, 2002). This model extends the embedded processes model by differentiating the FA within the FA proper, and the region of direct access (RDA). While the FA holds only the one cognitive representation which is actually being processed, the RDA is a limited-capacity fast-access system responsible for the maintenance of several representations that are task-relevant, and ready for selection into the FA. The concentric model thus suggests a hierarchy of storage systems with functionally very different components. This hierarchy allows us to make very specific predictions about information transfer and usage within WM. However, the empirical evidence for the concentric models is limited to the study of a specialized WM task (the arithmetic updating task, Oberauer, 2002), which limits this model’s generalizability.
In this article, we seek to validate the concentric model with the use of standard WM tasks–complex span tasks and updating tasks–applied to several research domains. Before we present the studies, we elaborate on the concentric model in more detail.
The concentric model
The concentric model makes several basic assumptions about the structure of working memory and the function of its components:
-
The FA is thought to contain a single representation which is being currently processed, and to have the highest level of accessibility. Items are loaded into the FA from the RDA. Items in the a-LTM can be prevented from decay by “loading” them into the FA in a cyclical fashion (“rehearsal”).
-
The RDA contains 3-4 items which are thought to be especially relevant for the task at hand. Items can be “off-loaded” to the a-LTM if they are no longer relevant. Items in the RDA are immune to interference, which is the only mechanism to cause forgetting (Oberauer et al., 2012).
-
The a-LTM is potentially unlimited in capacity and contains representations activated over a certain threshold. Representations in the a-LTM may be activated either through their FA, or via activation spreading from other representations in the WM. Representations in the a-LTM can be degraded through interference.
The concentric model suggests that the functional organization of WM is aimed at supporting two major functions–information storage and processing. It also provides a hierarchy of storage systems (RDA and a-LTM), the exact meaning of which is to be clarified. A major problem with the validation of the concentric model is that its validity has only been checked against WM updating tasks which were especially designed for this purpose.
However, today there are several standard ways to measure WM. One is to use typical WM updating tasks like the n-back and the mental counters task (Garavan, 1998; Owen et al., 2005). The other, even more important, approach is to use complex span tasks like the operation span task (Turner & Engle, 1989).
Method
Below, we review some original research on the validation of the concentric models using standard WM tasks and different methodologies. Specifically, we will consider four lines of research: 1) experimental studies of WM structure using S. Sternberg’s additive factors paradigm; 2) factor analytic studies of WM structure; 3) a study of serial position effects in WM; and 4) a study of WM structure in a sample with LTM deficits. We will conclude with a general discussion of how our findings relate to the organization of WM.
Results
The structure of WM: Sternberg’s additive factors approach
Sternberg’s additive factors method (Sternberg, 1984) is a statistical approach to identifying independent processing stages in cognition. It suggests experimental manipulation of several factors, which are assumed to selectively influence a number of hypothetical processing stages. If the factors do not interact statistically (the factors are thus additive), it is concluded that the processing stages associated with them are indeed independent. Extending this logic to the problem of identifying separated components in WM, we suggested that statistical analysis of factors selectively influencing the hypothetical components of WM may reveal the structure of WM (Velichkovsky, 2016; Velichkovsky et al., 2015). Specifically, factor additivity would suggest that the corresponding components can be differentiated, and that they function independently of each other. This logic was applied to the analysis of WM components suggested by the concentric model: the FA, the RDA, and the a-LTM.
In one of our studies (Velichkovsky, Nikonova, & Rumyantsev, 2015), we used the most standard tasks for the assessment of WM functions–the complex span tasks (e.g. Conway et al., 2005). These tasks combine storage of an item set in WM with performing an additional processing task. The main outcome measured by the task is the average probability of reporting the correct item in the correct serial position. Processing task complexity was thought to selectively influence the FA. The between-items interference in the storage task was thought to selectively affect processing in the a-LTM (as the RDA is assumed to be immune to interference in the concentric model). Finally, the WM load (the set size) was manipulated to include between two and six elements to affect both the RDA and LTM. This was plausible since the concentric model assumes a strict limit of 3-4 elements for the RDA (Oberauer, 2002), which means that the a-LTM is used for item storage when this limit is exceeded. The concentric models and the additive factors method allowed two specific predictions to be made about factor interactions in this experimental design:
-
Processing complexity should be independent of both interference and WM load, indicating that the FA differs from the RDA and the a-LTM.
-
WM load and interference should interact, indicating that the RDA and the a-LTM can be differentiated with respect to their sensitivity to interference.
In the study, two span tasks were used–the operation span task (Turner & Engle, 1989) and the parity judgment span task (Lepine et al., 2005). In the operation span task, consonant storage was combined with equation verification. Processing complexity was manipulated by the complexity of the equation verification. Two well-established complexity effects were used: the value effect (verification considered easier if the operands are less than 5), and the odd-even effect (verification considered easier if the parity of the true and displayed answer does not match) (Lemaire & Fayol, 1995). Interference was manipulated by using phonological similarity: consonants were varied according to the number of matching phonological features; those with two overlapping phonological features were considered to interfere to a greater extent (Schweppe et al., 2011). WM load was manipulated by presenting sequences of item sets in ascending and descending order (two to six items and six to two items). It was found that the complexity factor did not interact with either the load or interference factors, as predicted.
It was also found that the load factor interacted with the interference factor, again as predicted. This interaction was driven by the fact that the negative interference effect on storage efficiency was present only for loads over three items.
Both a priori hypotheses were thus supported. Exactly the same results were found in the experiment with the parity judgment task. In both experiments it was also found that increasing the WM load to over 3-4 items led to a significant drop in recall performance.
These results allow us to come to two major conclusions. First, processing of information in WM seems to be independent of storage, as there is no systematic interaction between processing complexity and factors affecting storage. It is tempting to interpret these results in structural terms in that the FA may be considered to be shielded from storage components. Second, these results suggest that storage in WM is realized by two distinct systems. One is a limited-capacity system which is insensitive to interference and provides a reliable storage of items (the RDA, in the terms of the concentric model). Another is a system which is sensitive to interference and less reliable. The second system is involved when there are more items to be maintained than is possible for the RDA to hold.
It is tempting to associate this second storage system with the a-LTM, as the above description closely fits the functional characteristics of the a-LTM, as suggested by the concentric model. There thus is a storage hierarchy in WM; the most accessible item is held in the FA, several items are reliably held in the RDA, and there is much less reliable storage in the a-LTM for the rest of the relevant information. In the Discussion section, we will consider why such a storage hierarchy may have evolved for adaptive purposes. For now, it’s sufficient to say that the specific predictions drawn from the concentric model were supported by complex span tasks’ data.
In another study we replicated the approach used above with updating tasks, specifically the mental counter task (Miyake et al. , 2000) and the n-back task (Owen et al., 2005). Updating tasks require the subject to maintain a set of items in memory, and to dynamically change their content; they are considered prototypical tasks for assessing WM functioning. We manipulated processing complexity, WM load, maintenance duration, and interference.
In the mental counter task the subjects had to count colored figures and react if a specific colored figure was presented forthe third time. The updating thus consisted in incrementally activating a mental counter for a color each time the color was presented. Complexity was manipulated by changing the required increment (+1 in the simple condition, +3 in the complex condition). WM load varied between four (within the RDA limits) and six (over the RDA limits) items. For each stimulus it was also registered how many stimuli were presented since the last presentation of this color (that is, measuring how long the corresponding counter was held in WM).
It was found that the complexity factor did not interact with either the WM load or maintenance duration. It was also found that the WM load interacted with maintenance duration for both accuracy and RT. The duration-dependent error and RT increase was larger for WM loads of six items than for WM loads of four items. These results are in full accord with those obtained for complex span tasks, and extend them by showing that the a-LTM may be also sensitive to time-related decay.
In the n-back task the subjects had to react if the current stimulus matched that presented npositions before. Processing complexity was manipulated by changing the identification task (identity or parity match). Interference was manipulated by using either numerically highly distinct digits (selected from 1 to 9) or numerically similar digits (selected from 5 to 9). WM load was manipulated by using 1-, 2, and 3-back conditions. The results matched those obtained for complex span tasks and for the mental counters task. The complexity factor did not interact with either interference or WM load, as the concentric model predicted. Interference and WM load did interact as predicted. To be precise, this interaction, driven by the negative effects of interference, was only observed in the 3-back condition.
In general, the results of the updating task also suggest independence of processing in the FA from information storage, and the existence of two storage components. One component is routinely used for the storage of small amounts of information (about 3-4 items) and is immune to interference and (possibly) time-related decay. The second component is recruited for the storage of larger amounts of information, and is susceptible to interference and time-related decay. These storage components correspond to the RDA and the a-LTM.
The structure of WM: A factor analytic approach
Previous studies used an experimental approach to the study of WM structure. Another approach is to investigate the structure of correlations between different WM tasks. Closely related to Baddeley’s WM model, this approach has previously been used to identify modality-specific storage systems within WM (Hale et al., 2011; Giofre et al., 2013), or to differentiate the central executive from storage systems (Kane et al., 2007). We sought to apply this approach to the validation of the concentric model. WM tasks of several types (complex span tasks, continuous span tasks, and updating tasks) were employed in order to sample WM functions with different processing and storage requirements. We were specifically interested in checking whether the correlation structure of different WM tasks allows for the identification of latent factors corresponding to WM components, as suggested by the concentric model. The number and content of latent factors was thus the primary research question. It was also of interest whether WM factors are independent of, or correlate with, each other.
In the study the subjects performed complex span tasks (operation span and counting span, Case et al., 1982) and continuous span tasks (parity judgment span and letter reading span, Lepine et al., 2005), as well as updating tasks (n-back and mental counters task). Continuous span tasks are span tasks with an extremely simplified processing subtask (like parity judgment or reading aloud letters from the native alphabet). This task class has the advantage that its performance does not depend on the ability to solve a complex processing subtask like equation verification. Continuous span tasks, like complex span tasks, were shown to reliably measure WM capacity (Barrouillet & Lepine, 2005). Recall accuracy for the maintenance subtask and processing accuracy and RT were registered for the span tasks, and accuracy (hits) and RT were registered for the updating tasks. Several models differing in the number of factors and factor loadings were devised according to theoretical considerations, and submitted to confirmatory factor analysis to assess model fit (fit indexes computed with the sempackage in the R statistical computing environment, Fox, 2006).
Specifically, Model 1 contained a single factor (corresponding to the unitary models of WM), Model 2 contained two factors, and Model 3 contained three factors (corresponding to the concentric model). Model fit was assessed via χ2, CFI, RMSEA, and SRMR fit indexes (see Table 1for results).
Table 1. Fit indexes for the structural models (see models’ descriptions in the text). Fit index values within admissible range (Brown, 2006) are in bold.
|
Model |
c2(df), p |
CFI |
SRMR |
RMSEA |
|
Model 1 |
62.3(20) <0.01 |
0.55 |
0.13 |
0.21 |
|
Model 2 |
47(18)<0.05 |
0.69 |
0.13 |
0.18 |
|
Model3 |
19.6(16)>0.05 |
0.96 |
0.12 |
0.07 |
|
Model4 |
18.1(15)>0.05 |
0.97 |
0.1 |
0.07 |
|
Model5 |
18(14)>0.05 |
0.96 |
0.11 |
0.08 |
In order to determine the number of factors, we compared Models 1, 2, and 3. According to Table 1,Model 1, with a single WM factor, shows the worst fit. Model 2, with two factors, also inadequately describes the data according to all fit indexes. It is notable that the factors in Model 2 were related significantly and positively (β=0.56), suggesting that some additional factors may explain the shared variance. Model 3, with three factors, provided a much better fit with insignificant χ2 and good CFI and RMSEA values. The SRMR value was somewhat out of range, indicating that further improvement was possible for the model.
Thus the model with three factors clearly outperformed the other models. We further studied the question of the independence of factors. To this end we computed fit indexes for eight models, describing all possible combinations of the presence/absence of relationships between the three factors. Only three of the eight models converged on a solution: Model 3 (assuming total independence of the factors); Model 4 (a positive correlation between Factor 1 and Factor 2, β=0.21); and Model 5 (a positive correlation between Factor 1 and Factor 2, and a positive correlation between Factor 1 and Factor 3, β=0.003). Table 1reveals that Model 4 provided a better fit than Models 3 and 5, and was the only model with all fit indexes in the acceptable range (Fig. 1). It is notable that the path coefficient between Factors 1 and 3 is very close to zero in Model 5. If it is set to zero, Model 5 is indistinguishable from Model 4. Thus, Factors 1 and 2 seem to be positively related, while Factor 3 is independent of other factors in the best fitting model.
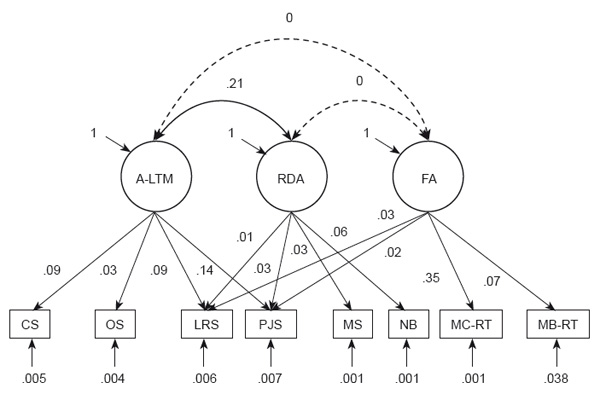
Figure 1.Model 4 (for more details, see the text). CS=counting span, OS=operation span, LRS=letter reading span, PJS=parity judgment span, MC=mental counters (accuracy), NB=n-back (accuracy), MC-RT=mental counters (RT), NB-RT=n-back (RT).
Factor 1 in Model 4 was loaded by recall accuracy in complex span tasks and continuous span tasks. As these tasks have the heaviest WM storage load (and the FA and the RDA are mostly used for processing and storage of intermediary results, especially in complex span tasks), this factor can be associated with the a-LTM. Factor 2 was loaded by continuous span tasks and accuracy of the updating tasks. Continuous span task have less processing demands, thereby making the use of the RDA for processing less probable. Furthermore, updating tasks also presumably use the RDA for the storage of the small number of items being updated (two items for 2-back and four items for the mental counters version used in this study). Factor 2 may thus be associated with the RDA.
Factor 3 is loaded by the continuous span tasks and the speed of the updating tasks. In interpreting the content of this factor, it should first be noted that continuous span tasks optimize the balance between storage and processing, and thus are indicative of both WM functions. It is also notable that the speed of updating is indicative of more dynamic processing (an updating operation is performed at each stimulus presentation during updating tasks, Botto et al., 2014), while updating accuracy is indicative of more items in storage in WM. For instance, in the n-back task, responses are not guessed only if the nth item is indeed stored in WM. Therefore, Factor 3 can be associated with the FA, the component of WM responsible for information processing.
The three factors in the best-fitting Model 4 correspond to the three WM components suggested by the concentric model: a processing component and two storage components. The storage components differ in the memory load they are able to handle, with the a-LTM handling more information. The a-LTM also seems to be engaged when the RDA is occupied with handling intermediary results for the processing task. These results corroborate the experimental data reported above. For instance, they also show that processing is in a sense independent of storage in the WM, since the FA factor doesn’t correlate with the storage factors. On the other hand, both the RDA and a-LTM factors correlate positively, indicating a functional relationship between them. We assume that the relationship between a-LTM and RDA factors may be driven by the presence of information exchange mechanisms between them. It is possible that information is “off-loaded” into the a-LTM from the RDA if it either doesn’t fit within the limits of the RDA, or is not considered relevant for the task at hand. Evidence for such “off-loading” was presented by Oberauer (2002) who showed that an item set initially encoded into the RDA can be off-loaded into the a-LTM upon presentation of a cue.
A similar information transfer from the RDA to the a-LTM was also shown with the directed forgetting paradigm (Fawcett & Taylor, 2012). It is perfectly possible that information transfer may occur in the opposite direction (from the a-LTM to the RDA) as previously irrelevant items may be required for the solution of the task at hand. The storage hierarchy in WM may thus be characterized by dynamic information transfer between its components, optimizing the amount of information maintained and its accessibility.
Serial position effects in WM
Serial position effects are observed in immediate recall tasks, and were used in the context of the modal memory model to support the distinction between long-term and short-term memory. These effects can be used to assess the structure of WM and validate the concentric model. In one study, subjects performed the operating span task (a complex span task) and the parity judgment span task (a continuous span task) with WM loads in the 2 to 6 items range. While these tasks are structurally very similar, they differ in the complexity of the processing subtask. In the operating span task, the processing subtask (equation verification) is relatively difficult and requires controlled attention. In the parity judgment span task (parity judgment for a short series of digits) the processing subtask is relatively easy and automatic. We were interested in answering two research questions: 1) whether there are serial position effects during the performance of WM tasks, and 2) whether serial position effects depend on the processing complexity. To this end we assessed both primacy and recency effects based on the relationship between recall accuracy and serial position.
The results suggest that there are pronounced serial position effects during WM tasks (the dependence of recall accuracy on serial position is statistically significant). Items in the middle serial position are poorly recalled. It is tempting to associate the primacy effects with the off-loading of items in excess of the RDA storage limits into the a-LTM (see above), while it is also tempting to associate recency effects with reliable storage of last items in the RDA. Serial position effects are in accord with the storage hierarchy suggested by the concentric model.
However, a more important result is the modulation of serial position effects by the complexity of the processing subtask. First, complex processing leads to a significant reduction of the primacy effect. Second, complex processing also leads to an increased recency effect. In support of these claims, it was found that there was no primacy effect in the operation span task, while there was a significant primacy effect in the parity judgment task. It was also found that the recency effect in the operation span task was significantly higher than in the parity judgment task.
These results suggest that the transfer of information is dependent on the processes and resources also employed by the processing subtask. That is, at least the transfer of information from the RDA to the a-LTM may be dependent on domain-general attention resources. The dependence of storage and processing in WM on general cognitive resources is a common idea in theories of WM (Towse & Hitch, 1995; Vergauwe et al., 2012). Investing resources in an attention-demanding task like equation verification thus prevents information items from being transferred from the RDA to the a-LTM, which negates the primacy effect.
However, the results also suggest that there is a dynamic allocation of cognitive resources within WM with the aim of optimizing both processing and storage efficiency. When the transfer of information into the a-LTM is precluded, storage in the RDA is boosted to compensate for it. This suggests a role of domain-general cognitive resources also in RDA storage, which also casts doubts on the simple notion of the RDA consisting of a small number of discrete slots. On the contrary, information storage in the RDA may be mediated by attentional resources, and thus RDA capacity may be subject to functional variations (Brose et al., 2012).
On the whole, the serial position data suggest that WM contains storage and processing components; that storage components form a storage hierarchy; that storage and processing components may deploy shared cognitive resources; and that components are selectively activated in WM in order to optimize both storage and processing performance. This view is in agreement with the concentric model, but allows for its extension to accommodate general domain cognitive resources and a regulative system for their dynamic allocation.
WM in people with LTM deficits
The structure of WM as suggested by the concentric model (and, specifically, the storage hierarchy) can be effectively studied in people with long-term memory deficits. The APOE-4 genotype is marked by the presence of the allele ε4 of the apolipoprotein E gene. This genotype is the major genetic risk factor for the development of Alzheimer’s disease in old age (Raber et al., 2005). There is considerable research on the cognitive profile of healthy APOE-4 carriers which has led to contradictory conclusions. Cognitive performance in young healthy APOE-4 carriers is usually indistinguishable from that in carriers of other genotypes. Healthy APOE-4 carriers may also outperform carriers of other genotypes on some cognitive tasks. However, large-scale meta-analytic studies systematically suggest that APOE-4 carriers have deficits in episodic long-term memory, which is often compensated for by increased cognitive control (Lancaster et al., 2017; Wisdom et al., 2011).
In a study, we assessed WM and its relationship in a sample of healthy APOE-4 carriers and age-matched controls (for details, see Velichkovsky, Roshchina, & Selezneva, 2015) to more fully understand the workings of WM when LTM is not functioning properly. To assess WM, the operation span task (two to six items) and the n-back task (2-back) were administered, along with a battery of cognitive control tasks.
It was found that performance on the operation span and n-back tasks didn’t differ between carriers and non-carriers, which suggests typical WM functioning in the carriers. Correlational analyses indicated, however, that the cognitive mechanisms of the WM task performance may differ between the carriers and non-carriers. For instance, it was found that operation spans for different set sizes correlated in the non-carriers, but not in the carriers, indicating a large variety in task execution mechanisms in the latter group. It was also found that operation span and n-back results correlated in the non-carriers but not in the carriers. This again suggests that while in the non-carriers WM tasks execution mechanisms are very consistent, such consistency is absent in the carriers. It was further found that while operation span in the non-carriers correlates with the antisaccade task (an attention control task), such correlations are absent in the carriers.
This is an intriguing result because WM tasks (especially complex span tasks like the operation span task) have been shown to strongly correlate with executive attention tasks like the antisaccade task (Engle, 2002). In this respect it is notable that n-back performance correlated with antisaccade performance in both the carriers and non-carriers. This dissociation may be interpreted in light of the fact that the 2-back task used in this study mostly relies on the RDA for items storage, while storage in the operation span task often exceeds the typical capacity limits of the RDA, and requires the a-LTM for item maintenance. As the a-LTM may be deficient in the carriers, they may use idiosyncratic strategies for the execution of the operation span task, which may thus not exhibit the correlation characteristic of the non-carriers. There are no such idiosyncratic strategies in the execution of the n-back task by the carriers as RDA is intact in them.
These results further corroborate the storage hierarchy view suggested by the concentric model. A fully intact storage hierarchy may be preserved in the non-carriers. This hierarchy includes a short-term memory component (RDA) and a long-term memory component (a-LTM). The latter is used more and more with the progressive increase of the WM load. In the carriers, the a-LTM component is compromised due to a general deficit in episodic LTM in this population. Importantly, the failure of the a-LTM does not preclude the carriers from exhibiting normal performance in WM tasks, especially the operation span task. This may be achieved by the recruitment of RDA resources, better cognitive control, or other specific strategies compensating for the inefficiency of the storage hierarchy. These findings are in strong agreement with the idea of the dynamic resource allocation to the components of WM proposed in the previous section. The functional organization of WM seems to actively compensate for the inefficiencies of selected components optimizing storage and processing during the execution of WM tasks. This again suggests a role for a regulatory component responsible for dynamic resource allocation to be included in the concentric model of WM.
Discussion
Several studies were presented, with the aim of validating the concentric model of WM (Oberauer, 2002). The studies used complex span WM tasks and WM updating tasks, both of which are the gold standard for measuring WM functions (Conway et al., 2005). The studies showed that predictions derived from the concentric model can be largely supported by the data. Below, we consider several of the studies’ results and discuss general implications for the theory of WM.
The results imply that WM contains a specialized processing component, which corresponds to the FA identified in the concentric model. Processing in the FA was shown to be independent of information storage in the WM. This follows from the processing complexity factor being systematically statistically independent of the factors affecting storage in the WM. Processing/storage independence may make adaptive sense. Assuming that there are common cognitive resources shared between processing and storage in WM (Towse & Hitch, 1995), the problem arises as to how to prioritize resources in cases where they are functionally or constantly depleted. A priority for processing makes it possible to search for solutions in a dynamic situation even if storage is undermined. Therefore it makes perfect sense to shield processing from the peculiarities of storage implementation. It should be noted that previous correlational studies have also shown a separation of processing from storage in WM (Barrouillet & Camos, 2007; Duff & Logie, 2001; Vergauwe et al., 2014), and suggested that these WM functions are differentially related to cognitive abilities (Unsworth et al., 2009). WM may thus have a modular architecture, with processing and storage modules functioning independently but influencing each other through a set of interfaces (Fodor, 1983).
The results also suggest that there are two functionally different storage systems in WM. These storage systems closely correspond to the distinction between RDA and a-LTM made by the concentric model. One storage system (the RDA) is capable of maintaining only a very limited number of elements (about four items), as evidenced by the absence of interference effects with loads below four items, and a marked decrease in WM recall accuracy for loads over three/four items. This is in strong agreement with research on WM capacity limits, which suggests a “new magic number” of four items (Cowan, 2001). Cowan (2001) reviews an impressive array of research showing that WM capacity was previously overestimated, and that WM capacity converges on about four items in experimental paradigms that preclude mnemonic strategies from better encoding WM content or its transfer to LTM.
On its face, the present result, may be interpreted as indicating storage in the RDA, without the transfer of information to a-LTM (this is precluded by the manipulations described in Cowan, 2001). It is notable that the concentric model also suggests a limit of four items for the RDA (Oberauer, 2002). A related line of research is being pursued by studies of relational complexity (Halford et al., 2005) which suggest that humans can only process relations between four variables. We will consider below why such a stringent capacity limit for RDA may still have adaptive value.
Beside capacity limits, the RDA is marked by its assumed insensitivity to interference effects (Oberauer, 2002). The absence of interference effects in some components of WM is a matter of debate. Some authors argue that parts of WM/short-term memory are immune to interference (Dempster & Cooney, 1982; Halford, Maybery, & Bain, 1988; Tehan & Humphreys, 1995), especially for loads below four items (which relates these findings to the capacity of the FA and the RDA). Other researchers suggest that the FA (in the broader sense including the RDA, Cowan, 1999) is as susceptible to interference as any other memory system (Carrol et al., 2010; Ralph et al., 2011; Shipstead & Engle, 2013).
Our data suggest that the limited-capacity storage system may be immune to interference, as interference effects were observable only outside of this storage system. It should be noted that this result was shown for complex span and updating tasks, which differ from the tasks used to assess the effects of interference, and are arguably more valid measures of WM functions. That items held in the RDA may be shielded from interference may have considerable adaptive value, if one assumes that the RDA’s functional role is the storage of several information items most relevant for the solution of the task at hand (in this respect the RDA is akin to the cache memory of modern computer architectures). It would be optimal if the RDA protected its items from decay due to interference or other factors, until they are used in the task-relevant processing, or are explicitly declared to be no-longer relevant and erased from RDA (Ecker et al., 2010; Maxcey & Woodman, 2014). However, it is possible that protection from interference is a dynamic property provided by the inhibitory mechanisms of cognitive control (Engle, 2002). Thus, the presence of interference effects may depend on the availability of inhibition, which may explain the ambivalent results concerning the role of interference in capacity-limited storage.
The second storage system in WM (a-LTM in the concentric model’s terms) is less capacity-limited. Given the limitations of our study, we couldn’t test for capacity limits of this storage system. The embedded process theory (Cowan, 1999) suggests that there are no such structural limits, and that storage in the a-LTM is limited only by finite activation resources. This view strongly corresponds to the idea that LTM has no storage limits, and that representations can be activated in LTM not only by their activation via the FA, but also due to automatic processes of spreading activation.
The present results further indicate another important feature of the a-LTM; it isprone to interference. This makes the a-LTM a typical memory system, and strongly suggests that it is indeed implementedwith the help of LTM mechanisms (see below). Our data also show that the a-LTM is recruited for WM storage only when the capacity limits of the RDA are exceeded by WM storage requirements. This suggests a two-tier storage architecture (“a storage hierarchy”), which is able to satisfy different storage requirements while maintaining quick accessibility of several decay-protected items, and still maintaining access to indefinitely large amounts of information potentially relevant for the solution of the task at hand.
The storage hierarchy view on WM storage which is explicated above, leads to the conclusion that WM storage is partly dependent on LTM storage mechanisms. The involvement of LTM mechanisms in WM has gained some support recently. For instance, research shows clear hippocampal involvement into the execution of WM tasks (the hippocampus being a structure traditionally associated with long-term episodic memory). Faraco et al. (2011) showed hippocampal recruitment during complex span tasks. Hippocampal activation was observed during the operation span task which contrasted to no hippocampal activation during a mental arithmetic task (which is a WM task akin to the processing subtask of the operation span but lacks its storage requirements). Öztekin et al. (2009) suggested a role for the hippocampus during retrieval of items not held in the FA. Leszczynski (2011) reviewed several studies on hippocampal involvement in WM and also suggested that is activated during WM maintenance. The hippocampus can also be involved in WM encoding and updating (Spellman et al., 2015).
Thus, the hippocampus as a LTM-related structure is consistently involved in various aspects of WM, with its involvement in information storage being best documented. This supports behavioral data (for instance, Unsworth et al., 2012) in suggesting that LTM mechanisms are involved in WM. WM is thus not a separate memory system strictly different from LTM. It is a functional system which recruits short-term and long-term memory mechanisms according to the storage/processing requirements as they evolve during the execution of the current task.
Why could the two-tier storage hierarchy be adaptive? First, it can be assumed that RDA capacity limitations are determined by the basic brain architecture (Cowan, 2001)–for instance, by the restrictions imposed by the neurons needed to fire synchronically while maintaining WM content. This leaves only a little capacity for fast-access reliable storage in the RDA, and it is easy to see that this capacity should be used to store the most relevant bits of information. The second storage system would provide access to larger data sets at the cost of slower access and less reliable storage. Thus, the two-tier hierarchy may have grown out of the difficulty of constructing a high-capacity fast-access reliable storage system.
Second, the low capacity of the RDA may be in itself an advantage, if items have to be selected into the FA for further processing (and it seems they have to be selected, Garavan, 1998; Oberauer, 2002). As selection processes are linearly dependent on the size of the set to be selected from, it is advisable to keep the set small if the selection has to be performed quickly. Optimizing selection-for-processing speed is especially important for WM, as it is primarily a system for the support of goal-directed actions. Thus, while increasing RDA capacity may be costly from the brain architecture point of view, it may not even be necessary if selection speed is to be optimized. In this respect the two-tier hierarchy may be an optimal compromise between access speed and information volume. Of course, such an architecture benefits from the putative information exchange mechanisms which enable the transfer of information between the levels of the storage hierarchy (consider the correlation between the a-LTM and the RDA in Fig. 1).
Our results on serial position effects further suggest that there may be a reciprocal relationship between the storage and processing components of the concentric model. This may be based on the use of common resources for the execution of specific WM tasks. For instance, the reduction of primacy effects by complex processing which we have observed, indicates that information transition between the RDA and the a-LTM may be resource-consuming. If such resources are diverted to processing in the FA, the off-loading of information items from the RDA to the a-LTM can be prohibited. There is already independent evidence that information transfer within WM storage systems is resource-consuming (Fawcett & Taylor, 2012).
An additionally significant result is the increase of the recency effect which complements the reduction of the primacy effect. This seems to support the view of WM as functional system. Allocation of resources within WM is not static but dynamic; the activation of different WM components is tailored according to the dynamics of task’s requirements. Overall, the dynamics of WM functioning and resource allocation optimize storage andprocessing depending on what is more relevant for achieving behavioral goals. This suggests the existence of a control module within WM which regulates the goal-directed resource allocation between WM components. The concentric model lacks such a component, or implicitly embeds it within the FA. The idea of WM as a dynamically regulated functional system is further supported by our data on WM functioning in the APOE-4 carriers, where deficiency in the a-LTM component leads to the functional reorganization of WM tasks performance.
Given that the concentric model gets some empirical support, it is important to relate it to Baddeley’s multicomponent WM model, which has for decades dominated WM theory, and for which there is a large amount of evidence. It seems that the concentric model and the multicomponent model are not incompatible but rather complementary.
First, the multicomponent model considers its “slave” (storage) systems to be unitary while the concentric models stress that there are different representational states (Zokaei et al., 2014) of items held in the storage systems. A valuable conclusion from the concentric model is that there is a complex storage hierarchy (or hierarchies) within WM. This conclusion should be incorporated into the multicomponent model.
Second, the multicomponent model stresses that storage in WM is modality-specific. That verbal, visual, and spatial storage processes are distinct within WM is empirically well-supported, but this aspect is lacking in the concentric model and has to be integrated into the concentric model by providing modality-specific storage hierarchies (which opens up an intriguing question of dynamic resource allocation between them, Vergauwe et al., 2012; Velichkovsky & Izmalkova, 2015).
Third, the multicomponent model lacks the FA as a specialized locus of processing, which the concentric model includes. This component should clearly be incorporated into the multicomponent model, given that the FA is clearly independent of storage in WM.
Fourth and last, it has already been shown that the concentric model needs a regulative module for the dynamic allocation of resources, which would enable it to be a functional system dynamically optimized to achieve the correct balance between storage and processing. Such a module is already present in the multicomponent model in the form of the central executive, which plays an important, if underspecified, role. It seems that to be a thorough model of WM, the concentric model will have to explicitly provide for a subsystem akin to the central executive. This would, for instance, explain the close empirical connections between WM capacity and executive control (Engle, 2002; Shipstead, Harrison, & Engle,2016).
Conclusion
Several studies were reviewed along with results of our recent experiments, with the aim of assessing the validity of the concentric model of WM (Oberauer, 2002; Shipstead, Harrison, & Engle,2016; Velichkovsky, Nikonova, & Rumyantsev, 2015; Velichkovsky, 2016). The model suggests that WM is comprised of a processing component–the FA, and two functionally distinct storage components–the RDA and the a-LTM. In the present analysis, we demonstrated that the predictions generated from the concentric model were largely supported by the results of several lines of research. In particular, it was found that the FA and the storage system function independently. Furthermore, the results supported the notion of the two storage systems forming a storage hierarchy, with the RDA being a capacity-limited reliable storage of several highly task-relevant items, and the a-LTM being an LTM-based capacity-unlimited storage system providing access to large amounts of potentially task-relevant information. Processing and task complexity in WM were shown to demand common cognitive resources. Overall, human WM proved to be a dynamic system which optimizes the activity of separate components according to the requirements of the current task.
Acknowledgements
This study was supported by the Russian Foundation for Basic Research, grant no. 16-06-00065.
References
Ackerman, P. L., Beier, M. E., & Boyle, M. O. (2005). Working memory and intelligence: The same or different constructs? Psychological Bulletin, 131, 30-60. doi: 10.1037/0033-2909.131.1.30
Baddeley, A. D. (1986). Working memory. Oxford: Oxford University Press.
Baddeley, A. D. (2012). Working memory: Theories, models, and controversies. Annual Review of Psychology, 63, 1-29.doi:10.1146/annurev-psych-120710-100422
Barrouillet, P. & Lepine, R. (2005). Working memory and children’s use of retrieval to solve addition problems. Journal of Experimental Child Psychology, 91, 183-204.doi: 10.1016/j.jecp.2005.03.002
Brose, A., Schmiedek, F., Lövdén, M., & Lindenberger, U. (2012). Daily variability in working memory is coupled with negative affect: the role of attention and motivation. Emotion, 12, 605-617.doi: 10.1037/a0024436
Brown, T. (2006). Confirmatory factor analysis for applied research. New York: Guilford Press.
Carroll, L. M., Jalbert, A., Penney, A. M., Neath, I., Surprenant, A. M., & Tehan, G. (2010). Evidence for proactive interference in the focus of attention of working memory. Canadian Journal of Experimental Psychology, 64(3), 208-214.doi: 10.1037/a0021011
Case, R., Kurland, M., & Goldberg, J. (1982). Operational efficiency and the growth of short-term memory span. Journal of Experimental Child Psychology, 33, 386-404.doi: 10.1016/0022-0965(82)90054-6
Conway, A., Kane, M., Bunting, M., Hambrick, D., Wilhelm, O., & Engle, R. (2005). Working memory span tasks: A methodological review and user’s guide. Psychonomic Bulletin & Review, 12(5), 769-786.doi: 10.3758/BF03196772
Cowan, N. (1999). An embedded-processes model of working memory. In A. Miyake & P. Shah (Eds.), Models of working memory. Mechanisms of active maintenance and executive control(pp. 62-101). Cambridge: Cambridge University Press.doi: 10.1017/CBO9781139174909.006
Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24,87-114.doi: 10.1017/S0140525X01003922
Daneman, M., & Carpenter, P. A. (1980). Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior, 19, 450-466.doi: 10.1016/S0022-5371(80)90312-6
Dempster, F. N. & Cooney, J. B. (1982). Individual differences in digit span, susceptibility to proactive interference, and aptitude/achievement test scores.Intelligence, 6,399-416.doi: 10.1016/0160-2896(82)90026-5
Ecker, U. K. H., Lewandowsky, S., Oberauer, K, & Chee, A. E .H. (2010). The components of working memory updating: An experimental decomposition and individual differences. Journal of Experimental Psychology, 36,170–189.doi: 10.1037/a0017891
Engle, R. (2002). Working memory capacity as executive attention. Current Directions in Psychological Science, 11,19-23.doi: 10.1111/1467-8721.00160
Faraco, C. C., Unsworth, N., Langley, J., Terry, D., Li, K., Zhang, D., … & Miller, L. S. (2011). Complex span tasks and hippocampal recruitment during working memory. Neuroimage, 55(2), 773-87.doi: 10.1016/j.neuroimage.2010.12.033
Fawcett, J. M. & Taylor, T. L. (2012). The control of working memory resources in intentional forgetting: Evidence from incidental probe word recognition. Acta Psychologica, 139, 84-90.doi: 10.1016/j.actpsy.2011.10.001
Fodor, J. A. (1983). Modularity of mind: An essay on faculty psychology. Cambridge, Mass.: MIT Press.
Fox, J. (2006). Structural equation modeling with the sem package in R. Structural Equation Modeling, 13,465-486.doi: 10.1207/s15328007sem1303_7
Garavan, H. (1998). Serial attention within working memory. Memory & Cognition, 26, 263-276.doi: 10.3758/BF03201138
Gathercole, S. E. & Alloway, T. P. (2008). Working memory and learning: A practical guide. Thousand Oaks: Sage Press.
Giofre, D., Mammarella, M., & Cornoldi, C. (2013). The structure of working memory and how it relates to intelligence in children. Intelligence, 41, 396-406.doi: 10.1016/j.intell.2013.06.006
Hale, S., Rose, N., Myerson, J. Strube, M., Sommers, M., Tye-Murray, N., & Spehar, B. (2011). The structure of working memory abilities across the adult life span. Psychology and Aging, 26,92-110.doi: 10.1037/a0021483
Halford, G. S., Baker, R., McCredden, J. E., & Bain, J. D. (2005). How many variables can humans process? Psychological Science, 16,70-76.doi: 10.1111/j.0956-7976.2005.00782.x
Halford, G. S., Maybery, M. T., & Bain, J. D. (1988). Set-size effects in primary memory: An age-related capacity limitation? Memory & Cognition, 16,480-487.doi: 10.3758/BF03214229
Kane, M., Conway, A., Hambrick, D., & Engle, R.W. (2007). Variation in working-memory capacity as variation in executive attention and control. In A. R. A. Conway, C. Jarrold, M. J. Kane, A. Miyake & J. Towse (Eds.), Variation in working memory(pp. 21-48). New York: Oxford University Press.
Lancaster, C., Tabet, N., & Rusted, J. (2017). The elusive nature of APOE ε4 in mid-adulthood: Understanding the cognitive profile.Journal of the International Neuropsychological Society, 23,239-253.doi: 10.1017/S1355617716000990
Lemaire, P. & Fayol, M. (1995). When plausibility judgments supersede fact retrievals: The example of odd-even effect on product verification. Memory & Cognition, 23(1), 34-48.doi: 10.3758/BF03210555
Lepine, R., Bernardin, S., & Barroillet, P. (2005). Attention switching and working memory spans. European Journal of Cognitive Psychology, 17(3), 329-345.doi: 10.1080/09541440440000014
Leszczynski, M. (2011). How does hippocampus contribute to working memory processing? Frontiers in Human Neuroscience, 5,168.doi: 10.3389/fnhum.2011.00168
Maxcey, A. & Woodman, G. (2014). Can we throw information out of visual working memory and does this leave informational residue in long-term memory? Frontiers in Psychology, 5,294.doi: 10.3389/fpsyg.2014.00294
Oberauer, K. (2002). Access to information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(3), 411-421.doi: 10.1037/0278-7393.28.3.411
Oberauer, K., Lewandowsky, S., Farrell, S., Jarrold, C., & Greaves, M. (2012). Modeling working memory: An interference model of complex span. Psychonomic Bulletin Review, 19(5), 779-819.doi: 10.3758/s13423-012-0272-4
Öztekin, I., McElree, B., Staresina, B.P., & Davachi, L. (2009). Working memory retrieval: Contributions of the left prefrontal cortex, the left posterior parietal cortex, and the hippocampus. Journal of Cognitive Neuroscience, 21, 581-593.doi: 10.1162/jocn.2008.21016
Owen, A. M., McMillan, K. M., Laird, A. R., & Bullmore, E. (2005). N-Back working memory paradigm: A meta-analysis of normative functional neuroimaging studies. Human Brain Mapping, 25,46-59.doi: 10.1002/hbm.20131
Raber, J., Huang, Y., & Ashford, J. W. (2005). ApoE genotype accounts for the vast majority of AD risk and AD pathology. Neurobiology of Aging, 25, 641-650.doi: 10.1016/j.neurobiolaging.2003.12.023
Ralph, A., Walters, J. N., Stevens, A., Fitzgerald, K. J., Tehan, G., Surprenant, A. M., … & Turcotte, J. (2011). Immunity to proactive interference is not a property of the focus of attention in working memory. Memory & Cognition, 39(2), 217-30.doi: 10.3758/s13421-010-0030-7
Schweppe, J., Grice, M., & Rummer, R. (2011). What models of verbal working memory can learn from phonological theory: Decomposing the phonological similarity effect. Journal of Memory and Language, 64,256-269.doi: 10.1016/j.jml.2010.11.006
Shipstead, Z. & Engle, R. W. (2013). Interference within the focus of attention: Working memory tasks reflect more than temporary maintenance. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(1), 277-289.doi: 10.1037/a0028467
Shipstead, Z.,Harrison, T. L., & Engle,R. W. (2016). Working memory capacity and fluid intelligence: Maintenance and disengagement. Perspectives on Psychological Science, 11(6), 771-799.doi: 10.1177/1745691616650647
Spellman, T., Rigotti, M., Ahmari, S. E., Fusi, S., Gogos, J. A., & Gordon, J. A. (2015). Hippocampal-prefrontal input supports spatial encoding in working memory. Nature, 522(7556), 309-14.doi: 10.1038/nature14445
Sternberg, S. (1984). Stage models of mental processing and the additive-factor method. Behavioral and Brain Sciences. 7,82-84.doi: 10.1017/S0140525X00026285
Tehan, G. & Humphreys, M. S. (1995). Transient phonological codes and immunity to proactive interference. Memory & Cognition, 23(2), 181-191.doi: 10.3758/BF03197220
Towse, J. & Hitch, G. (1995). Is there a relationship between task demand and storage space in tests of working memory capacity? Quarterly Journal of Experimental Psychology, 48, 108-124.doi: 10.1080/14640749508401379
Turner, M. & Engle, R. (1989). Is working memory capacity task dependent? Journal of Memory & Language, 28, 127-154.doi: 10.1016/0749-596X(89)90040-5
Unsworth, N., Redick, T., Heitz, R., Broadway, J., & Engle, R. (2009). Complex working memory span tasks and higher-order cognition: A latent-variable analysis of the relationship between processing and storage. Memory, 17,635-654.doi: 10.1080/09658210902998047
Unsworth, N., Spillers, G., & Brewer, G. (2012): Working memory capacity and retrieval limitations from long-term memory: An examination of differences in accessibility. The Quarterly Journal of Experimental Psychology, 65(12), 2397-2410.doi: 10.1080/17470218.2012.690438
Velichkovsky, B. B. (2016). Short- and long-term storage components in working memory. International Journal of Psychology, 51(S1), 180.
Velichkovsky, B. B. & Izmalkova, A. I. (2015). Vlijanie nagruzki na verbalnuju rabochuju pamjat pri glazodvigatelnoj aktivnosti v uslovijah vypolnenija zadanija zritelnogo poiska [Effect of verbal working memory load during the oculomotor activity in visual search]. Eksperimentalnaya psikhologiya [Experimental Psychology], 8(2), 21-35.
Velichkovsky, B. B., Nikonova, E. Yu., & Rumyantsev, M. A. (2015). Struktura rabochej pamjati: effekty uvelichenija kolichestva informacii, uslozhnenija obrabotki i interferencii [The structure of working memory: Effects of increased information load, processing complexity, and interference]. Psikhologicheskii zhurnal [Psychological Journal], 36(3), 38-48.
Velichkovsky, B. B., Roschina, I. F., & Selezneva, N. D. (2015). Cognitive control and memory in healthy apoe-ε4 carriers with a family history of Alzheimer’s disease.Psychology in Russia: State of the Art, 8(1), 4-13.doi: 10.11621/pir.2015.0101
Vergauwe, E., Dewaele, N., Langerock, N., & Barrouillet, P. (2012). Evidence for a central pool of general resources in working memory. Journal of Cognitive Psychology, 24, 359-366.doi: 10.1080/20445911.2011.640625
Wisdom, N. M., Callahan, J. L., & Hawkins, K. A. (2011). The effects of apolipoprotein E on non-impaired cognitive functioning: A meta-analysis. Neurobiology of Aging, 32, 63-74.doi: 10.1016/j.neurobiolaging.2009.02.003
Zokaei, N., Ning, S., Manohar, S., Feredoes, E., & Husain, M. (2014). Flexibility of representational states in working memory. Frontiers in Human Neuroscience, 8,853.doi: 10.3389/fnhum.2014.00853
To cite this article: Velichkovsky B. B.(2017). The concentric model of human working memory: A validation study using complex span and updating tasks. Psychology in Russia: State of the Art, 10 (3), 74-92.
The journal content is licensed with CC BY-NC “Attribution-NonCommercial” Creative Commons license.









