Mathematical fluency in high school students
Abstract
This article presents the results of a study of mathematical fluency in high school students. We provide a definition of mathematical fluency and illustrate the relevance of the research by presenting an overview of studies examining mathematical fluency development and its relationship with success in mathematical disciplines.
A computerized test “Problem Verification Task” (Tosto et al., 2013) was administered to 692 high school students from one public secondary school (grades 9/10/11: n = 336/210/146) in the Moscow region. The stimuli consisted of 48 elementary arithmetic equations along with answer options. To indicate a correct answer, participants were instructed to press the corresponding key on the keyboard as quickly as possible.
Two-way ANOVA was used to estimate grade and sex similarities and differences in mathematical fluency at the high school level.
The current study has two primary findings: (1) students differed in math fluency across grades, and (2) there were no sex differences in mathematical fluency at the high school level. ANOVA exhibited significant differences in mathematical fluency among all three groups of students at grades 9, 10 and 11 with a 19% effect size. These results may be associated with the accumulating effects of the educational process: high school students in each subsequent year of schooling demonstrate a higher level of mathematical fluency on average compared to the previous year. At the same time, we observed no sex differences in mathematical fluency at the high school level. The results are discussed in terms of educational effects.
Received: 07.09.2016
Accepted: 13.12.2016
Themes: Educational psychology
PDF: http://psychologyinrussia.com/volumes/pdf/2017_1/psych_1_2017_7.pdf
Pages: 95-104
DOI: 10.11621/pir.2017.0107
Keywords: mathematical fluency, mathematical achievement, education, high school age, sex differences
Introduction
The concept of fluency in psychology is traditionally associated with the dynamic characteristics of the thinking process and is used as a psychometric index in a range of diagnostic tests, for example, tests of creative thinking (Runco et al., 2010). In this context, fluency is defined as a specific combination of accuracy and response speed, and it characterizes competence in certain fields (Binder, 1996; Therrien, 2004). In experimental studies, the concespt of fluency was studied primarily in relation to reading and is associated with the development of basic reading skills (Vygotsky, 1983; Kuhn et al., 2010; hasbrouck, Tindal, 2006; Therrien, 2004; Fuchs et al., 2001 и др.). L.S. Vygotsky wrote that reading speed is directly related to depth of understanding and text comprehension. In particular, Vygotsky noted that “... during fast reading, comprehension turns out to be better ... and the comprehension speed is related to faster pace reading” (Vygotsky, 1983, p. 192).
However, the focus of attention has recently shifted toward mathematical fluency, which is defined as the ability to perform basic mathematical operations quickly and accurately; this ability leads to success in mathematical disciplines (Singer-Dudek, greer, 2005; Floyd et al., 2003). Fluency in arithmetic is essential for the success of students in everyday life because it serves as a foundation for mathematical applications such as time and money (Smith et al., 2011). There are three main reasons to investigate mathematical fluency. First, fluency in basic mathematical operations is essential to mastering higher-order mathematical skills, such as multi-step problems in algebra (Smith et al., 2011). Second, due to the lack of effort required and more frequent successes, schoolchildren who respond automatically typically have less anxiety in math (Poncy et al., 2007). Third, high levels of mathematical fluency are maintained longer, and students are better able to resist distractions and stay on task longer (Rhymer et al., 2000).
Indeed, experimental studies aimed at optimizing the process of assimilation and further application of basic mathematical skills are of great social and practical value in terms of the requirements of national educational standards, daily activities (Codding et al., 2009), and development of the knowledge-intensive sectors of society (Butterworth, Kovas, 2013).
Studies show that not only people with low levels of cognitive development experience difficulties in learning mathematics (geary et al., 2000; Siegel, 1988). One reason for lack of success in mathematics might be low mathematical fluency (Binder 1996; Ramos-Christian et al., 2008). This relationship might stem from the incorrect distribution and/or limitations of cognitive powers; in other words, a person spends most of his cognitive abilities at the primary stages of problem-solving, leaving only the minimum necessary to perform the more complicated steps that lead to a successful solution (Delazer et al., 2003).
It has been shown that while solving mathematical problems of increased complexity, for example, people with low mathematical fluency must first make maximum use of their cognitive resources (e.g., attention, memory) to perform basic arithmetic operations, limiting the use of those resources in further problem solving (Ramos-Christian et al., 2008; Skinner et al., 2005; Dehaene, 2011). In turn, individuals with high levels of mathematical fluency manage quickly and accurately to perform initial calculations, saving more cognitive resources for completing the task (Dehaene, 2011). It was also demonstrated that students with higher levels of mathematical fluency exhibit low levels of mathematical anxiety (Cates, Rhymer, 2003) and greater motivation for mathematical activities (Codding et al., 2009), contributing to higher achievement in the field.
The relationship between mathematical fluency and success in mathematical disciplines has led to increased interest in the development of educational technologies aimed at boosting mathematical fluency. There are many experimental studies focused on comparing the effectiveness of training programs aimed at improving mathematical fluency among students and school children (hulac et al., 2012; Smith et al., 2011; Bramlett et al., 2010; Codding et al., 2009; Seethaler & Fuchs, 2005). Mathematical fluency is usually assessed with the mathematical fluency subtest of the Woodcock-Johnson achievement test (Woodcock et al., 2001).
Mathematical fluency is often associated with sex differences in mathematical achievement. It is reported that men perform mathematical calculations better and faster than women (Wai et al., 2009; Royer et al., 1999). however, a meta-analysis of sex differences in solving standardized arithmetic tasks, which was conducted with a sample of US students, did not show any differences between mean values for boys and girls (hyde et al., 2008). however, this study reported somewhat greater variability indices for boys than for girls.
There are few studies of the etiology of mathematical fluency. One behavioral-genetic study was designed to evaluate the contributions of genetic and environmental factors to the relationship between mathematical fluency and other characteristics of mathematical success (Petrill et al., 2012; Malykh et al., 2012).
It should be noted that a substantial portion of the research on mathematical fluency was carried out with English-speaking samples from the U.S. and the UK, largely due to the support of the state educational authorities (e.g., The National Council of Teachers of Mathematics). Sometimes these investigations are a part of cross-cultural projects related to mathematical fluency. These studies have shown differences in how children successfully solve elementary mathematical problems, with Chinese children frequently outperforming American peers (geary et al., 1996; Siegler, Mu, 2008; Vasilyeva et al., 2015). In a study carried out with the participation of Russian preschoolers, higher performance on addition tasks in elementary arithmetic tests was also observed in Chinese children compared to Russian and English children (Rodic et al., 2015). These results were associated with mathematically oriented pre-school education and/or with specific features of numeric language, e.g., the shorter pronunciation of Chinese numbers (Rodic et al., 2015; Vasilyeva et al., 2015; Aunio et al., 2006).
It should be noted that most existing studies examined developmental changes in mathematical fluency in elementary school children (e.g., Bartelet, 2014; Cow-an at el., 2011; geary, 2011; Carr & Alexeev, 2011). This finding may reflect a belief that mathematical fluency undergoes major development during elementary school years and does not improve significantly at an older age. however, high school math includes more complex problems, which provide practice in computation, so it is possible that mathematical fluency continues to improve at that age through experience.
The aim of this study is to examine age and sex differences in the mathematical fluency of Russian high school students. We propose that on average, high school students in each subsequent year of schooling will demonstrate significantly higher mathematical fluency compared to the previous year.
Method
Sample
Research participants included 692 schoolchildren in grades 9–11 of public secondary school aged from 14.17 to 18.67 years (Mean = 16.53; SD = .88). Students in grade 9 accounted for 48.6% of the total number of participants (336 students, 50% boys), grade 10 — 30.3% (210 students, 45.7% boys) and grade 11 — 22.5% (146 students, 39.7% boys). The students were recruited from one public secondary school in a greater-Moscow region. The education curriculum at the school follows a standardized state program.
Measure
All participants completed a computerized test «Problem Verification Task» (PVT test). The stimuli consist of 48 arithmetic problems with a proposed answer (Tosto et al., 2013). All problems included elementary arithmetic equations, for example ‘8 : 2 = 4’, ’12 + 50 = 62’, ‘44 – 18 = 24’, ’13 × 4 = 47’, etc. In half of the trials, the answer is correct; in the other half, the answer is wrong. Every item is presented in the same format: a mathematical equation is shown at the top of the screen, and the keys ‘Right’, ‘Wrong’ and ‘I don’t know’ are shown beneath a mathematical equation. The timer is shown in the left corner of the screen. The image below shows the example items with a correct (a) and an incorrect answer (b) from the PVT test (see Fig. 1).
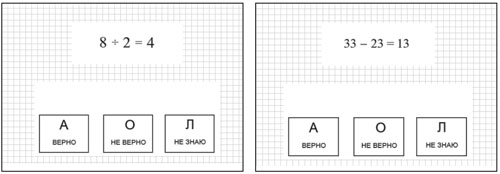
Figure 1. Example of «Problem Verification Task» items
Participants decide whether the answer proposed is correct as quickly as possible by pressing the corresponding keys on the keyboard. The task starts with instructions and a practice trial that includes two items. The “time-out” for a response in this task is 10 seconds. A time bar appears at the top of the screen to show the participant the time remaining. After a response is given, the problem is presented with no delay. It is possible to interrupt the task halfway-through and resume it later. The task records the accuracy and reaction time of a correct response.
Data collection was conducted in the educational institution, strictly following the protocol and under the constant supervision of an experimenter. Analysis of the results was carried out using anonymized personal data.
Results
The paper analyzed the mathematical fluency score, calculated as the number of correct responses, with a limit of 10 seconds for each task. First, the data were analyzed in terms of norms and distributions for the PVT test at each grade. Table 1 presents descriptive statistics by grade.
Table 1. Descriptive statistics for Problem Verification Task
|
|
Males |
Females |
|
Grade 9 |
34.81 (7.9) |
34.24 (6.8) |
|
Grade 10 |
40.80 (5.8) |
39.49 (4.5) |
|
Grade 11 |
42.28 (4.8) |
41.89 (3.7) |
Table 1 shows the average number of correct answers for the PVT test. The lowest possible score on the test is 0; the maximum possible is 48. As illustrated in Table 1, mean scores for mathematical fluency increased with years of schooling. A decrease in the standard deviation in grade 11 indicates a trend towards concentration and regularity of mathematical fluency scores in students at grade 11. The male students in each grade demonstrated, on average, higher means and larger standard deviations than female students.
Second, we investigated sex and age differences in mathematical fluency at high school age. Effects of a year of schooling (grades 9, 10, 11) and sex (male, female) were assessed by two-way ANOVA. The dependent variable was PVT test scores.
To test the hypothesis that all dependent variables have the same variance, we used Levene's test for equality of variances. The p-value was below .05, indicating variance inequality on the test indicator.
Table 2. Inferential statistics for Problem Verification Task
|
Effect |
SS |
F |
p |
ƞ2 |
|
‘Years of Schooling’ |
6208.42 |
80.72 |
0.00 |
0.19 |
|
‘Sex’ |
84.43 |
2.20 |
0.14 |
0.00 |
|
Effects interaction |
22.60 |
0.29 |
0.75 |
0.00 |
Table 2 shows that the effect of the factor «Years of schooling» was statistically significant for mathematical fluency (η2 = .19, p = .00). The results of multiple comparisons with the Bonferroni correction showed significant differences between all the analyzed groups (p < .01). At the same time, the lowest mean value was shown in the group of students in grade 9 (Mean = 34.53, SD = 7.4). The best results on the PVT test were demonstrated by students in grade 11 (Mean = 41.04, SD = 4.2). The means and standard deviations for male and female students are presented in Table 1.
The gender effect was not significant for mathematical fluency (p > .05). Thus, males and females do not differ in mathematical fluency at high school age.
Discussion
The present study investigated the age and sex differences in mathematical fluency at high school age.
On one hand, the results may show the cumulative effects of the educational process — on average, students in each subsequent academic year have had a greater number of classes and mathematical practice out of school compared to previous grade levels. It is especially important for students in grade 11, when all Russian students take the Unified State Exam, which includes math. Indeed, frequent use of elementary or complex mathematical operations can improve mathematical fluency (Hulac et al., 2012; Bramlett et al., 2010). For example, it was demonstrated that the method “Cover, Copy, and Compare”, which is based on behaviorism, is an effective tool in improving mathematical fluency (Poncy et al., 2010; Skinner et al., 1997). A statistically significant difference was found between groups with different levels of mathematical fluency in terms of the effectiveness of their spatial ability and levels of visuospatial memory (Tikhomirova et al., 2013). These results demonstrate that mathematical fluency can be learned through education (as in this study) or through specially designed training sessions (in accordance with the theoretical analysis presented above).
On the other hand, the improvement of mathematical fluency from grades 9 to 11 may be associated with maturational changes. however, numerous studies demonstrate that education is one of the most important factors in age-related cognitive development (e.g., Brinch & Galloway, 2012). In the current study, we used a cross-section associational design and have not analyzed age-related differences.
Regarding sex differences, males and females do not differ in mathematical fluency in high school. It should be noted that in one of our previous studies on a small sample of Russian high school students, we also found that the gender effect on mathematical fluency was not statistically significant (Tikhomirova & Kovas, 2013). The results of this study conducted on a larger sample showed no sex differences in mathematical fluency in Russian high school students. This result does not replicate the results of the study of sex differences in mathematical fluency in American students (Geary et al., 2000). It was reported that, compared to girls, boys perform significantly better on elementary arithmetic tasks. This discrepancy in results may be due to cross-cultural differences in education systems.
In general, existing studies have found a bi-directional relationship between mathematical fluency and mathematical achievement. A large body of studies have reported that mathematical fluency is a predictor of mathematical success (e.g., Singer-Dudek, Greer, 2005; Smith et al., 2011). At the same time, studies describing the effects of training sessions have demonstrated effects of mathematical exercises on mathematical fluency (Hulac et al., 2012; Bramlett et al., 2010). In other words, mathematical fluency and success in mathematics may be reciprocally interrelated. Longitudinal research is needed to establish the precise developmental course of the links between mathematical fluency and mathematical achievement at school age.
At the same time, according to international mathematical ratings (e.g., PISA, TIMMS), there are stable, cross-cultural differences in mathematical achievement in schoolchildren. Therefore, it seems promising to conduct a cross-cultural, longitudinal study in different grades to detect individual and cross-cultural differences in the structure of the relationships between mathematical fluency and mathematical achievement and to determine the specific cultural, linguistic, and educational factors contributing to the observed cross-cultural differences.
Acknowledgments
This study was supported by a grant from the Russian Science Foundation, project No. 15-18-30055.
References
Aunio, P., Niemivirta, M., hautamaki, J., Van Luit, J.E.h., Shi, J., & Zhang, M. (2006). Young children’s number sense in China and Finland. Scandinavian Journal of Educational Research, 50(5), 483–502. doi: 10.1080/00313830600953576
Bartelet, D., Vaessen, A., Blomert, L., & Ansari, D. (2014). What basic number processing measures in kindergarten explain unique variability in first-grade arithmetic proficiency? Journal of experimental child psychology, 117, 12–28. doi: 10.1016/j.jecp.2013.08.010
Binder, C. (1996). Behavioral fluency: Evolution of a new paradigm. The Behavior Analyst, 19(2), 163–197.
Bramlett, R., Cates, g. L., Savina, E., & Lauinger, B. (2010). Assessing effectiveness and efficiency of academic interventions in school psychology journals: 1995–2005. Psychology in the Schools, 47(2), 114–125.
Brinch, C.N., & Galloway, T.A. (2012). Schooling in adolescence raises IQ scores. Proceedings of the National Academy of Sciences, 109(2), 425–430. doi: 10.1073/pnas.1106077109
Butterworth, B., & Kovas, Y. (2013). Understanding neurocognitive developmental disorders can improve education for all. Science, 340(6130), 300–305. doi: 10.1126/science.1231022
Carr, M., & Alexeev, N. (2011). Fluency, accuracy, and gender predict developmental trajectories of arithmetic strategies. Journal of Educational Psychology, 103, 617–631. doi: 10.1037/a0023864
Cates, g. L., & Rhymer, K. N. (2003). Examining the relationship between mathematics anxiety and mathematics performance: An instructional hierarchy perspective. Journal of Behavioral Education, 12(1), 23–34. doi: 10.1023/A:1022318321416
Codding, R. S., Chan-Iannetta, L., Palmer, M., & Lukito, G. (2009). Examining a classwide application of cover-copy-compare with and without goal setting to enhance mathematics fluency. School Psychology Quarterly, 24(3), 173–185. doi: 10.1037/a0017192
Codding, R.S., hilt-Panahon, A., Panahon, C.J., & Benson, J.L. (2009). Addressing mathematics computation problems: A review of simple and moderate intensity interventions. Education and Treatment of Children, 32(2), 279–312. doi: 10.1353/etc.0.0053
Dehaene, S. (2011). The number sense: How the mind creates mathematics. OUP USA.
Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Locky, A., Treib, T., & Benke, T. (2003). Learning complex arithmetic-an fMRI study. Cognitive Brain Research, 18, 76–88. doi: 10.1016/j. cogbrainres.2003.09.005
Floyd, R.g., Evans, J.J., & Mcgrew, K.S. (2003). Relations between measures of cattell-horncattell (ChC) cognitive abilities and mathematics achievement across the school-age years. Psychology in Schools, 40, 155–171. doi: 10.1002/pits.10083
Fuchs, L.S., Fuchs, D., Hosp, M.K., & Jenkins, J.R. (2001). Oral reading fluency as an indicator of reading competence: A theoretical, empirical, and historical analysis. Scientific Studies of Reading, 5(3), 239–256. doi: 10.1207/S1532799XSSR0503_3
Geary, D.C., Bow-Thomas, C.C., Liu, F., & Siegler, R.S. (1996). Development of arithmetical competencies in Chinese and American children: Influence of age, language, and schooling. Child Development, 67, 2022–2044. doi: 10.2307/1131607
Geary, D.C., Saults, S.J., Liu, F., & Hoard, M.K. (2000). Sex differences in spatial cognition, computational fluency, and arithmetical reasoning. Journal of Experimental child psychology, 77(4), 337–353. doi: 10.1006/jecp.2000.2594
Geary, D.C. (2011). Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Developmental psychology, 47(6), 1539. doi: 10.1037/a0025510
Hasbrouck, J., & Tindal, G.A. (2006). Oral reading fluency norms: A valuable assessment tool for reading teachers. The Reading Teacher, 59(7), 636–644. doi: 10.1598/RT.59.7.3
Hulac, D.M., Dejong, K., & Benson, N. (2012). Can students run their own interventions?: A self-administered math fluency intervention. Psychology in the Schools, 49(6), 526–538. doi: 10.1002/pits.21614
Hyde, J.S., Lindberg, S.M., Linn, M.C., Ellis, A.B., & Williams, C.C. (2008). Gender similarities characterize math performance. Science, 321(5888), 494–495. doi: 10.1126/science.1160364
Kuhn, M.R., Schwanenflugel, P.J., & Meisinger, E.B. (2010). Aligning theory and assessment of reading fluency: Automaticity, prosody, and definitions of fluency. Reading Research Quarterly, 45(2), 230–251. doi: 10.1598/RRQ.45.2.4
Malykh, S.B., Tihomirova, T.N., & Kovas, Yu.V. (2012). Individualnyie razlichiya v sposobnostyah k obucheniyu: vozmozhnosti i perspektivyi psihogeneticheskih issledovaniy [Individual differences in learning abilities: opportunities and prospects of behavioral genetics]. Voprosyi obrazovaniya [Issues in Education], 4, 186–199. doi: 10.17323/1814-9545-2012-4186-199
Petrill, S.A., Logan, J., hart, S., Vincent, P., Thompson, L., Kovas, Y., Plomin, R. (2012). Math fluency is etiologically distinct from untimed math performance, decoding fluency, and untimed reading performance: Evidence from a twin study. Journal of Learning Disability, 45(4), 371–381. doi: 10.1177/0022219411407926
Poncy, B.C., McCallum, E. & Schmitt, A.J. (2010). A comparison of behavioral and constructivist interventions for increasing math-fact fluency in a second-grade classroom. Psychology in the Schools, 47(9), 917–930. doi: 10.1002/pits.20514
Ramos-Christian, V., Schleser, R., & Varn, M.E. (2008). Math fluency: Accuracy versus speed in preoperational and concrete operational first and second grade children. Early Childhood Education Journal, 35, 543–549. doi: 10.1007/s10643-008-0234-7
Rhymer, K.N., Dittmer, K.I., Skinner, C.h., & Jackson, B. (2000). Effectiveness of a multi-component treatment for improving mathematics fluency. School Psychology Quarterly, 15, 40–
51. doi: 10.1037/h0088777
Rodic, M., Zhou, X., Tikhomirova, T., Wei, W., Malykh, S., Ismatulina, V., ... & Kovas, Y. (2015). Cross-cultural investigation into cognitive underpinnings of individual differences in early arithmetic. Developmental Science, 18(1), 165–174. doi: 10.1111/desc.12204
Royer, J.M., Tronsky, L.N., Chan, Y., Jackson, S.J., & Marchant, H., III. (1999). Math-fact retrieval as the cognitive mechanism underlying gender differences in math test performance. Contemporary Educational Psychology, 24, 181–266. doi: 10.1006/ceps.1999.1004
Runco, M.A., Millar, g., Acar, S., Cramond, B. (2010). Torrance tests of creative thinking as predictors of personal and public achievement: A fifty year follow-up. Creativity Research Journal, 22(4), 361–368. doi: 10.1080/10400419.2010.523393
Seethaler, P.M., & Fuchs, L.S. (2005). A drop in the bucket: Randomized controlled trials testing reading and math interventions. Learning Disabilities Research & Practice, 20(2), 98–102. doi: 10.1111/j.1540-5826.2005.00125.x
Siegel, L.S. (1988). Evidence that IQ scores are irrelevant to the definition and analysis of reading disability. Canadian Journal of Psychology, 42, 201–215. doi: 10.1037/h0084184
Siegler R.S., Mu Y. (2008). Chinese children excel on novel mathematics problems even before elementary school. Psychological Science, 19(8), 759–763. doi: 10.1111/j.1467-9280 .2008.02153.x
Singer-Dudek, J., & Greer, R.D. (2005). A long-term analysis of the relationship between fluency and the training and maintenance of complex math skills. Psychological Record, 55, 361–376.
Skinner, C.H., Mclaughlin, T.F., & Logan, P. (1997). Cover, copy and compare: A self-managed academic intervention effective across skills, students and settings. Journal of Behavioral Education, 7(3), 295–306. doi: 10.1023/A:1022823522040
Skinner, C.H., Pappas, D.N., & Davis, K.A. (2005). Enhancing academic engagement: Providing opportunities for responding and influencing students to choose to respond. Psychology in the Schools, 42, 389–403. doi: 10.1002/pits.20065
Smith, C.R., Marchand-Martella, N.E., & Martella, R.C. (2011). Assessing the effects of the rocket math program with a primary elementary school student at risk for school failure: A case study. Education and Treatment of Children, 34(2), 247–258. doi: 10.1353/etc.2011.0011
Therrien, W.J. (2004). Fluency and comprehension gains as a result of repeated reading. Remedial and Special Education, 25, 252–261. doi: 10.1177/07419325040250040801
Tikhomirova, T.N., & Kovas, Yu.V. (2013). Vzaimosvyaz kognitivnyih harakteristik uchaschihsya i uspeshnosti resheniya matematicheskih zadaniy (na primere starshego shkolnogo vozrasta) [The relationship between cognitive characteristics and the success of solving mathematical tasks at high school age]. Psihologicheskij Zhurnal [Psychological Journal], 34(1), 63–73.
Tikhomirova, T.N., Malykh, S.B., Bogomaz, S.A., Sudneva, O.V., Kovas, Y. (2013). Prostranstvennoe myshlenie i pamyat u starsheklassnikov s razlichnym urovnem matematicheskoj beglosti [Spatial ability and spatial memory in high school students with different levels of mathematical fluency]. Teoreticheskaya i eksperimentalnaya psikhologiya [Theoretical and experimental psychology], 6(4), 99–109.
Tosto, M.G., Tikhomirova, T., Galajinsky, E., Akimova, K., & Kovas, Y. (2013). Development and validation of a mathematics-number sense web-based test battery. Procedia – Social and Behavioral Sciences, 86, 423–428. doi: 10.1016/j.sbspro.2013.08.591
Vasilyeva, M.,Laski, E., & Shen, C. (2015). Computational fluency and strategy choice predict individual and cross-national differences on complex arithmetic. Developmental Psychology, 51(10), 1489–1500. doi: 10.1037/dev0000045
Vygotsky, L.S. (1983). Istoriya razvitiya vysshih psihicheskih funkcij. Problemy razvitiya psihiki [The history of the development of higher mental functions]. In Sobraniye sochineniy: v 6 t. T. 3. [Collected works in 6 volumes. Vol. 3]. Moscow: Pedagogika. (Original work published 1960)
Wai, J., Lubinski, D., & Benbow, C. P. (2009). Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. Journal of Educational Psychology, 101(4), 817. doi: 10.1037/a0016127
Woodcock, R.W., Mcgrew, K.S., & Mather, N. (2001). Woodcock-Johnson III: Test of cognitive abilities. Itasca, IL: Riverside.
To cite this article: Tikhomirova T.N., Misozhnikova E.B., Malykh A.S., Gaydamashko I.V., Malykh S.B. (2017). Mathematical fluency in high school students. Psychology in Russia: State of the Art, 10(1), 95-104.
The journal content is licensed with CC BY-NC “Attribution-NonCommercial” Creative Commons license.










