Multivariable Objects for Stimulation of Young Children's Combinatorial Experimentation and Causal-Experimental Thought

Poddiakov, A.N. Lomonosov Moscow State University, Moscow, Russia

1. Introduction

It has become acknowledged recently that a most important direction of human cognitive development is the development of abilities at activities in complex multivariable dynamical environments. Educators try to design such systems of education, which could develop these abilities including combinatorial abilities, the ability to reason in causal nets as opposed to causal chains, the ability to predict non-linear dynamics and the ability to build optimal strategies of control, etc. (Demetriou et al., 1993; Dörner, 1997; Frensch & Funke, 1995; Spector, 2005; Voss, 2006). These abilities are crucial, e.g., in Combinatorial Science (CombiSci) applied for discovery of new target materials--biomaterials, catalytic materials, nanomaterials, etc., for researches in informatics, and in other domains.

Understanding of interacting structures of complex reality by experimentation is the main function of causal-experimental thought. This specialized structural system includes: combinatorial abilities as the cornerstone of the system; abilities to form complex hypotheses about interactions and causal connections between elements (variables); experimentation abilities (abilities to design experiments for testing the hypotheses); abilities to construct interpretative models (Demetriou et al., 1993).

Best cultural tools for education in areas of multivariable relations are complex didactic objects. They simulate and demonstrate active intelligent functioning, including simulation of situations of physical, biological and social multivariable net determination and self-determination. Children are experimenting with such an object by themselves, revealing multiple causal relations and creating virtual microworlds (Klahr & Simon, 1999; Schauble & Glaser, 1990; Strand-Cary & Klahr, 2008).

In more general terms, such objects specially designed for developing independent exploration and learning of children by stimulating the child’s problem-solving skills and the discovery of the object’s features, contain some didactic programs in implicit form. The programs are revealed during a child’s interaction with such an object. The structure and functioning of the object stimulate a sequential mutually-supporting increase: (a) in the variety and complexity of the child’s exploratory actions with regard to the object in question; and (b) in richer knowledge about it (Poddiakov N., 1995). I consider such didactic objects as a means to identify and control the zone of children’s proximal development. In a sense, these objects are substitutes for an adult, helping the child to learn and master some activity independently. Social interaction between the child and the adult takes place when the adult is absent but is replaced with a cultural tool (designed by the adult) as a substitute. Thus, these objects are a means of dialogue between the cultures of adults and children.

As for children’s combinatorial experimentation and causal-experimental thought, according to Piaget (Flavell et al., 2002), preschoolers (i.e., preoperational children) have neither well-expressed combinatorial abilities nor the ability to comprehend multivariable relationships. They can explore and comprehend only the simplest situations of clearly apparent interaction between two variables with two levels (i.e., situations not more complex than 2×2) (Demetriou et al., 1993). Yet Bruner wrote: “one can indeed imagine kindergarten games designed to make children more actively alert to how things affect or are connected with each other–a kind of introduction to the idea of multiple determination of events in the physical and the social world” (Bruner, 1966, p. 27).

My work is aimed at the following: a) formulation of heuristic rules for designing didactic objects stimulating preschoolers' combinatorial experimentation and causal-experimental thought, and designing the objects themselves; b)study of the preschoolers' cognitive activity (exploratory learning) aimed at the objects, and identifying their aptitude for combinatorial experimentation.

The study has been conducted for 16 years. A system of various didactic objects has been designed. The objects are complex, having many connections and interactions between their elements, and required complex combined (e.g., simultaneous) actions on their controls. These actions cause the object's reactions, which were considerably different from reactions on single actions. Participants were 623 children of 3-7 years old.

Heuristic rules for the objects' design, description of some of the objects, and experiments studying children's experimentation (“experimentation with experimentation”) are presented below.

2. Heuristic rules for design of multivariable objects for preschoolers

The following heuristic rules can be formulated to design a whole system of multivariable objects aimed at stimulating children’s combinatorial experimentation and causal-experimental thought.

1. The objects should contain implicit information related to, at least, three kinds of the adults’ ideas: (a) ideas about multivariable relations and scientific experimentation with them; (b) ideas about children’s cognitive abilities, potentials and interests; (c) ideas about aims of the dialogue including, on the one hand, development of the children’s abilities and, on the other hand, elaboration of all three kinds of the adults’ ideas.
2. Any of the objects should give a child an opportunity to raise various problems, i.e., problems, differing in aims, methods of their achievement, levels of complexity, etc.
3. The system should include objects with various compositions of subsystems of two types: (a) a subsystem with one-to-one relations and without interactions of variables; (b) a subsystem with the interactions of variables and not one-to-one relations. Representation of subsystems of both types, being in varying compositions, facilitates deeper comprehension of the multivariable objects and relations contained in the objects.
4. The system should include objects, differing in a level of objectification of the following parameters: (a) possible variables; (b) their combinations; (c) processes of the interactions of variables; (d) results of the interactions. These parameters can be clear or hidden, vary from a level of observable mechanical elements and their interactions to a level of variables and interactions that are given in a conventional verbal or symbolic way only (e.g., as a mathematical or logical rule), etc.
5. The simplest objects should be based on content well-known and clear for children, and include a minimum of interacting variables and simplest dependencies, characterizing the interactions.
6. The following objects facilitate children’s activity focused on combining variables and exploration of their interaction. The objects react to single actions by effects that are considered incomplete by the children. Combined actions cause an object’s reactions that are considerably different from the effects of the single actions. Namely, the effects of the single actions are integrated into some systems of visible interactions. As a child increases the variety of combined actions the object reveals more of its features that enable the child to make progress in comprehending this object.

These heuristic rules do not claim to be complete and universal. The system of objects, designed according to these rules, is open, i.e., one can bring new objects and withdraw or modify old ones, depending on research and practical targets.

Some of the objects and children’s activity with them are described below.

3. The mechanical device

3.1. Description of the Mechanical Device

The object called the mechanical device is a complex of mechanisms for transporting metal balls from the starting point to the final positions. Relations between the mechanisms are not one-to-one. (It should be noted that the real device is more simple than its verbal description. The object is interesting for children and can be comprehended by them.) Its body is a box with an incline (Fig. 1).

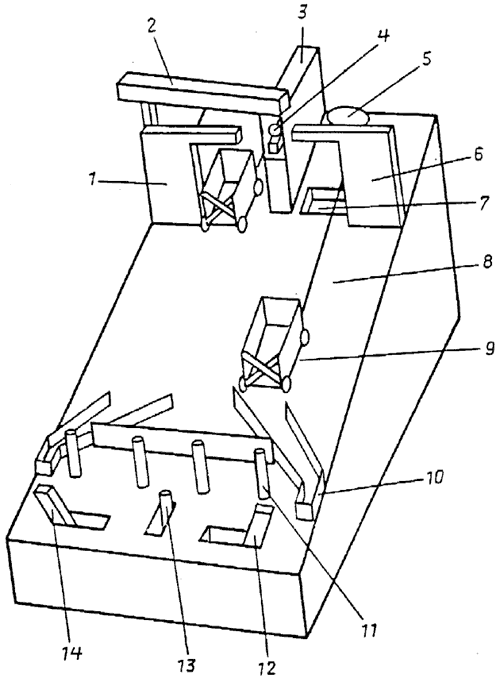
Figure 1. The Mechanical Device

1 – the left tower, 2 – the container, 3 – the central tower, 4 – the ball, 5 – the right pulley, 6 – the right tower, 7 – the right pit, 8 – the cord, 9 – the right cart, 10 – the right cul-de-sac, 11 – the right rod, 12 – the right handle, 13 – the central handle, 14 – the left handle

There is a control panel in the lower part of the inclined plane. The control panel has four rods, one central handle and two side handles. There is a working field with reacting elements in the higher part of the plane. The working field has: a) a central tower with a metal ball on a moving support in the higher part of the tower; b) two side towers; c) two carts connected with each other by a cord; d) two pulleys for the cord; e) two pits (each of them between the central tower and a side tower); f) four special lifts.

To throw the ball off the support one has to perform the following. The metal ball on the support must be moved from the central tower by moving the central handle from the distant to the near (or working) position. It is necessary to keep the handle in the working position, otherwise the moving support with the ball will go back into the tower. Moving a side (left or right) handle to the central handle makes a rod-shaped pusher move from a side (left or right) tower. The pusher is invisible until moving the handle and becomes visible during this action. The pusher hits the ball which falls down. Thus throwing the ball off requires combined actions on two handles to achieve an interaction between the pusher and the ball.

If the left cart is near the central tower, it is necessary to throw the ball into the cart by the pusher of the right tower using the central and right handles. If the right cart is near the central tower, it is necessary to use the central and left handles. If a child throws the ball to a side where there is no cart (e.g. to the right, but not to the left) the ball falls into a pit. Of course, the carts do not move. It is possible to take the ball from the pit with hands only. But if the ball falls into a cart, the latter moves down and the other cart moves up. The cart with the ball stays in the lower part of the working field and the empty cart stays between the central and side towers.

To unload the ball from a cart one must do the following. Each of the carts has two locks in the form of crossing bars (Fig. 2). By simultaneously pressing two rods in front of a cart one can make two lifts move up. The locks are lifted and the ball rolls from the cart to a small “culde-sac”. Pressing a single rod has no such effect because only one lock is lifted. Thus unloading the ball requires combined actions on two rods to achieve interaction between the lifts and the locks.

It is possible to take the ball from the cul-de-sac with hands and put it into the container of the central tower. The ball rolls through the container onto the moving support. Then all the operations can be repeated in a symmetrical variant, that is by throwing the ball into the other cart, moving both carts and rolling the ball to the other cul-de-sac.

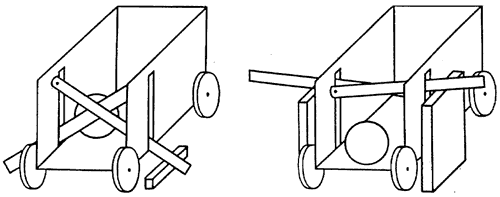
Figure 2. Unloading of the ball from the cart

The important difference between the mechanical and the calculating device is that the latter does not allow children to integrate effects of single actions into a system. The effects of single actions can not supplement each other in any way because they are the same – lighting of the first left window. But the mechanical device is a system including a hierarchy of subsystems. These subsystems can be integrated into different functional units by an interaction between reacting mechanisms. The initial and the most simple unit is throwing the ball off the support. It can be organized by an interaction between two subsystems: a) “central handle – moving support – ball” subsystem; b) “side handle – side pusher” subsystem. Also these subsystems can be integrated into another, non-effective functional unit “stopping the ball by a pusher”. Integration of the unit “throwing the ball off” and the “carts” subsystem results in a more complex functional unit responsible for loading the ball into a cart and moving both carts. Integration of this unit and two “rod–lift” subsystems results in the last unit responsible for rolling the ball from a cart to a cul-de-sac. Thus an important feature of children’s thinking must be comprehension of novel effects caused by combined actions.

3.2. Experiment with the Mechanical Device

Procedure. The device was explored by one child for not more than 20 min. The experimenter showed the device to the child and said that it was a toy. He also said that there is only one rule in the game: the child was allowed to handle the control elements only (handles and rods) and was not allowed to handle anything in the working field. If the child asked how he could play with the toy the experimenter evaded the question in a friendly way and suggested he should try out. If the child was not able to throw the ball off the support and his cognitive activity began to decrease the experimenter helped him with leading questions and prompts. They were used gradually for making comprehension of the object by a child easier: from the leading question about a possible function of the ball to showing how to use the handles correctly. If the child solved the problem successfully the experimenter stopped his intervention, otherwise he went on helping the child.

If the ball fell into a pit or rolled in a cul-de-sac the experimenter put it into the container again and the child could continue manipulations.

If the child could not throw the ball into a cart and threw it to a pit four times in succession the experimenter also used some sequence of leading questions and prompts.

Results and discussion. I describe the results of the experiment with this device in more detail than the results of experiments with other devices because The Mechanical Device is the most complicated, and a detailed consideration of the children’s activity with The Mechanical Device makes it easier to understand the rest of the experiments.

During the initial observation of the object the children supposed that the carts could move. They wanted to move the carts and thought that it could be done by handling control elements. For example, Igor K. (aged 5 years 9 months) said: “I understand why it is not allowed to handle this (he meant the working field). There are special handles for it. It is necessary to move a cart”. Anna V. (aged 5 years 1 month) asked the experimenter: “What must I handle to move the carts?” At the beginning the children more often than not utilized single actions on handles and rods. Of course, it did not result in moving the carts. But the children figured out relations between control and reacting elements. They could see the ball on the support, pushers and lifts moving. Also, they saw some reacting elements move towards other elements which were immobile at that time (e.g. a pusher moved towards the immobile ball). Comprehension of these situations encouraged the children to set a new target that is to make one element touch another. The information about relations between the control and reacting elements which had been obtained by single actions allowed preschoolers to find a way of achieving their goal, which was utilizing combined actions. So most of the children (18 participants or 90%) began to combine actions by themselves. They did it after an average of 11.9 single actions.

Three children performed their first combined action on handles correctly. Seventeen children could not discover the correct action immediately. They began to try out various interactions of reacting elements. The preschoolers utilized various combined actions on handles and attentively watched interactions of the ball and pushers: stopping the ball (which was moving) by a pusher (which had moved out), clutching the ball between the pushers, a collision of the pushers etc. During these actions the children often tried to draw the experimenter’s attention to some situations, they laughed if any interaction of elements seemed funny to them etc. This variety of children’s combined actions allowed us to draw the following conclusion. The preschoolers utilized various combined actions on control elements as a means of specific aim achievement. This aim was performing various actions on some reacting elements by other reacting elements. Thus it is possible to distinguish between two kinds of combinatorics of children’s actions: a) combinatorics of manual actions on control elements; b) combinatorics of actions on some reacting elements by other reacting elements.

Also, most of the participants acted on rods. They looked at moving lifts and opening locks of the lower (empty) cart. Children saw that single actions on rods made only one lock go up and they integrated both effects, that is they lifted both locks by simultaneously pressing both rods. It showed that the tendency to combine effects of single manual actions stimulated children to combine the manual actions themselves.

Ten found the adequate action to throw the ball off the support by themselves. They did it after 24.1 single and combined actions on average. The rest of the children needed some help. It should be emphasized that the necessary help included the experimenter’s questions or prompts referring to reacting elements only (e.g. the ball, the support, a pusher), but not to control elements. Children needed help to comprehend the adequate interaction between reacting elements. Soon after the children comprehended the “right” combination of the ball and a pusher they found the adequate action on handles by themselves. It confirmed the conclusion about the interaction between combinatorics of children’s manual actions and combinatorics of the actions’ effects.

Fourteen children threw the first ball into a cart. Six participants threw it into a pit and five of them did it 4 times in succession. The experimenter helped them. Finding the adequate actions on handles (with or without the help) allowed the participants to observe the most complex reaction of the device, that is falling of the ball into a cart, downward movement of this cart and upward movement of the other. It gave the preschoolers new important information about the object and methods of its control. By finding the adequate reaction the children achieved their main goal and so they showed satisfaction and often delight, joyfully shouting and clapping their hands etc.

This reaction of the device stimulated the preschoolers to set a new aim that is to unload the ball from the cart. Five participants solved this problem by randomly testing all control elements, 9 participants found the adequate combined actions on two rods at once, without any erroneous attempts and 6 children solved the problem at a medium level. Successful problem solving depended on efficacy of the child’s previous activity directed at rods, lifts and locks of the lower empty cart. Some children could not utilize efficiently the information obtained and they solved the problem at a low or medium level.

Thirteen children managed to throw the second ball off the support in the symmetrical variant at once, but 7 children had difficulty with this operation. Some preschoolers could not remember how the ball could be moved from the central tower, other participants remembered that actions had to be combined (!), but they did not remember what control elements had to be simultaneously acted on. They tried a pair of rods, the pair of side handles, a rod and the central handle etc. When a child moved the central handle he or she saw the ball moving. Then the child began systematic combinatorial sorting (!) of control element pairs. In each of the pairs one element (the central handle) was constant and the other element varied. This sorting considerably raised efficacy of the search for the adequate combined action, because it cut most of the erroneous pairs (i.e. the pairs without the central handle). Some children utilized the same systematic sorting when they searched for the method to unload the ball from a cart.

Results of children’s experimentation on the device were the following. Sixteen participants (80%) acquired method of its control at a high level: they either did not make any errors at all or made only a few errors being inattentive. They corrected their wrong actions immediately. Four children (20%) often made errors repeatedly and controlled the device at a lower level. But there was not anybody in the group who could not cope with the object at all.

Thus children’s experimentation on the object included figuring out features of element interactions resulting in a construction of various functional units and their integration into a whole working system with a specific function. During comprehending the device the preschoolers utilized various combined actions which allowed them to get novel qualitative effects of an interaction between variables, that is a visible interaction between reacting elements. Owing to these features of their activity the children formed knowledge about the object and methods of its control.

4. The calculating devices

4.1. Description of the Calculating Devices

Calculating Device-1 (Figure 3a) has 3 rods and 1 window with a picture behind a shutter. When any N rods are simultaneously pressed the shutter goes up making N/3 of the window area visible. Even 3-yearolds comprehend that increase of number of the pressed rods results in increase of the visible area of the picture. This object is simplest and can be used as introductory.

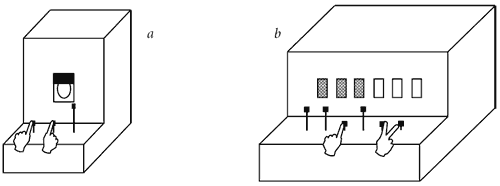
Figure 3. The Calculating Devices: a – Calculating Device-1; b – Calculating Device-2

Calculating Device-2 (Fig. 3b) realizes the same principle, but is more complex. It has a row of 6 rods and a parallel row of 6 dark windows with invisible pictures of popular tale characters. To light up the windows and make pictures visible it is necessary to press rods. What windows are illuminated depends on a number of rods pressed and does not depend on their location. The device can realize 2 variants (modes) of this general relationship. In the mode “Addition”, by simultaneously pressing any N rods N left windows are illuminated. For example, by pressing any single rod the first left window is illuminated, by pressing any two rods both the first and the second windows are illuminated etc. In the mode “Subtraction” simultaneous pressing any N rods illuminates 7-N right windows.

4.2. Experiment with the Calculating Device-2 (mode “Addition”)

Procedure. An experimenter suggested a child play with the new toy by her or himself. At the end of the experiment the adult suggested the child should perform tasks focused on causal relationships in the toy and possible actions on it. The experiment was individual and continued for a maximum of 20 min.

Participants: 30 children aged 5 years (15 boys and 15 girls).

Results and discussion. After the first combined pressing and the object’s new reaction (i.e., lighting of several windows) the children began to press other rods simultaneously. They found new combinations at an accelerated rate. The average intervals between the first pressing of one kind and the first pressing of the next kind were as follows:

• (1) 18.3 pressings between the first pressing of 1 and 2 rods;
• (2) 4.9 pressings between the first pressing of 2 and 3 rods;
• (3) 0.9 pressings between the first pressing of 3 and 4 rods;
• (4) 0.8 pressings between the first pressing of 4 and 6 rods;
• (5) 1.1 pressings between the first pressing of 6 and 5 rods.

As a rule, pressing of 5 rods was performed after pressing of 6 rods (!)

Some preschoolers performed series of actions. In these series a number of pressed buttons remained constant, but their location varied. It is important that 15 preschoolers (50%) counted the pressed rods and the illuminated windows. This created the necessary conditions for the children to comprehend the main quantitative relationship of the object’s functioning. At various levels of understanding, the preschoolers found out the mathematical relationship characterized by an interaction of several factors. In fact, the children comprehended that this interaction could be interpreted as an effect of one complex factor that is a number of pressed rods.

5. The triangle device

5.1. Description of The Triangle Device

The device is designed to give a preschooler an opportunity to see and perform all the possible combinations of 4 variables factors. This type of combinatorial thinking was considered achievable for adolescents only, not for preschoolers (Demetriou et al., 1993; Flavell, 2002).

The device has 3 buttons, being in apexes of the equilateral triangle drawn (Fig. 4). The buttons are in little drawn circles. There are two windows (i.e., near and distant), having the form of equilateral triangles with circles in the apexes too, in front of the buttons. The windows contain invisible pictures, which one can see by lighting them up. There is a toggle switch between windows, to the right of them. It can be oriented either to the near window or to the distant one. It determines the window, in which pictures can be lit.

Pressing any single button lights up a picture in the appropriate circle of the window, chosen by the switch. Pressing the left button lights up the left circle, pressing the right button lights up the right circle and pressing the top button lights up the top circle. Simultaneously pressing any two buttons lights up a rectangular stripe, connecting circles, and not the circles themselves. Simultaneously pressing all the three buttons lights up a triangle inside the window, but the circles and stripes remain dark.

The pictures form a system, based on the following principle. Each circle in the window contains a picture of an object. Each stripe, connecting two circles, contains a combination of both objects from these circles. The triangle inside the window contains combination of all the three objects.

In terms of the theory of control, the device is a multi-relational object that can be in 16 states. One of them is initial. The rest of them can be realized by 15 different single and combined actions, i.e., by complete combinatorial search for 4 controlling elements.

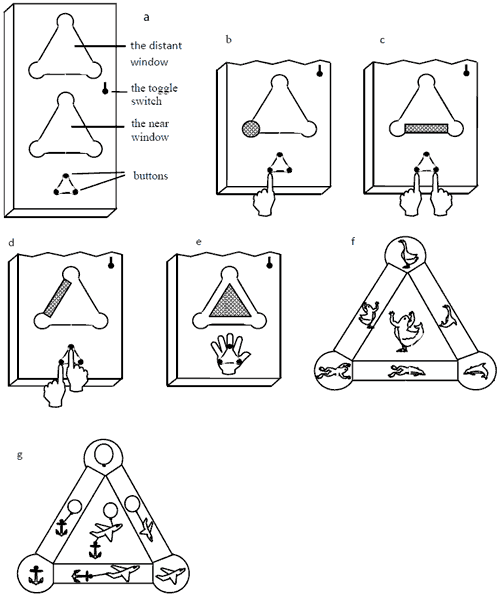
Figure 4. The “Triangle” Device stimulating children to perform complete combinatorial search for 4 control variables: a – top view; b–e – pressings of buttons and lights in the near window; f – pictures lighted in the near window, g – pictures lighted in the distant window

5.2. Experiment with The Triangle Device

Procedure was the same as the procedure of the experiment with the Calculating Device-2.

Participants: 60 children (20 children of 4 years, 20 children of 5 years, and 20 children of 6 years).

Results: 85% of the children of 4 years, 95% of the children of 5 years, and 85% of the children of 6 years found all the 15 possible states of the object, i.e., performed all the combinations of actions on the control elements and saw all the pictures. A number of actions, which the children made for the complete combinatorial search, varied from 25 (made by a girl aged 6 years) to 262 (made by a girl aged 4 years) and was equal to 103.5 on average. It was much more than the 15 necessary actions. (It should be noted that the experimenter did not pose any task to the children to decrease a number of actions.). Computer simulation of random actions on the controls gave 57.3 actions on average in 1000 experiments. But though the children made more actions than the program, their actions were not random. At the beginning the children pressed buttons one by one, then they began to press pairs of buttons, and after that they pressed all the three ones. This similarity of the strategies of all the participants could be accidental with probability less than 0.0000005%. Also, the children did not make inadequate actions, like pulling an electric wire, knocking on the device etc., which one could expect, for example, from the younger children. If one enters possibility of several such actions into the program, it will make many more actions till the end of the search because of combinatorial explosion.

It was a matter of principle that the children, beginning from the age of 4, could find and perform all the combinations of 4 variables (though not in the shortest exact logical sequence, but using the strategies accessible for them).

6. The matrix device

6.1. Description of The Matrix Device

The Matrix Device (Figure 5) has a row of 5 rods parallel to the bottom line and another 5 rods parallel to the left side of the box. Also, there is matrix of square windows covered with flaps. The latter can be opened by pressing rods.

In the mode “Tale characters”, 35 windows (matrix 6×6–1) contain pictures of characters from folk tales. When any rod is pressed, the window closest to the rod gets open. When two or more rods in both rows are simultaneously pressed, windows with coordinates determined by the pressed rods get open (Figure 5a-c).

In the mode “Shape × color multiplication”, there are 25 square windows integrated into a 5×5 matrix (Figure 5d). There are 5 square labels with pictures of geometric forms between the rods of the horizontal row and the windows of the bottom line, and 5 colored square labels between the rods of the vertical row and the windows of the left column. In the windows there are pictures of figures of corresponding shapes and colors. The pictures are concealed behind shutters and can be opened only by simultaneous pressings of rods. In this mode, no pictures can be made to appear by pressing rods in one row only.

6.2. A child’s individual experimentation with the Matrix Device

Mode: “Shape × color multiplication"

Procedure was the same that the procedure of the experiment with Calculating Device-2.

Participants: 90 children (30 children of 5 years, 30 children of 5 years, and 30 children of 9-10 years).

Results: 20% children aged 5 years, 50% children aged 6 years, and 93% children aged 9-10 years made ordered search for pairs of buttons, moving in the rows in succession. This class of strategies included a sufficiently exact variant of the odometer strategy (cf. English, 1993) in which minor items were buttons of one row (e.g., the horizontal row) and major items were buttons of the other row (e.g., the vertical row). Thus, the children used one of the main scientific principles of experimentation, i.e., varying one variable while keeping the others constant. Only those children, who had used these strategies, showed a high level of comprehension of the object functioning while performing tasks (Poddiakov A., 1994).

6.3. Children’s joint experimentation with the Matrix Device

Mode: “Tale characters”

Participants: 18 children (8 children aged 4 years, 4 children aged 5 years and 6 children aged 6 years).

Procedure: The experimenter suggested a pair of children play with the new toy on their own. He told them that there is only one rule in the game: one row of rods was for one child, the other row of rods was for the other child and the children could not press the other’s rods.

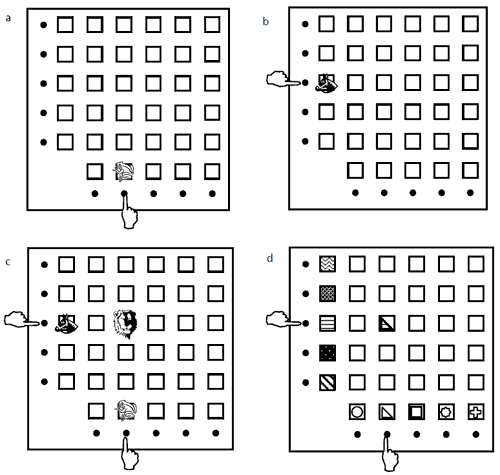The Matrix Device (top view)" />

Figure 5. The Matrix Device (top view): a–c – the matrix device in the mode “Tale characters”; d – the matrix device in the mode “Shape × color multiplication”

Results. In the first stage the children acted independently of each other. They pressed rods and looked at the pictures in the white windows. The second stage began when both children accidentally pressed their rods simultaneously and noticed a picture in a new open window.

Usually each of the children thought that this effect was caused by his or her own action. Some children said: “I have opened the window”. Some of their partners agreed with this. Yet others began to solve the question as to which of them in fact opened “problem” windows. For example, Seva P. (6;6) said: “I have opened a picture of Little Red Riding Hood”. Misha M. (6;9) answered: “No, it is I who has opened Little Red Riding Hood”. They began to argue angrily: “It is my Little Red Riding Hood!”, “No, mine!”, etc. But all of a sudden Seva found a way to show that he was right. He withheld his rod and said: “But I have closed your Little Red Riding Hood”. This was a very important moment. The child proved that s/he was a participant of the device control in equal rights by using not positive, but negative information (i.e., information about the rod withheld and the window closed). Usually children figure out “authorship”, e.g., in joint playing computer games by making more frequent and intensive actions, not by stopping them (Forman, 1986). Yet our object made the children invent a more advanced strategy. After that the children performed several pressings and withholdings and understood that opening of the pictures was a result of their joint and simultaneously performed manipulations (“We have done it together”). In the third stage of activity these children began to coordinate their aims and actions, talking with each other in a very polite way. (This transition from the mutual anger to the politeness was rather amusing.) Thus, the experiment has shown that joint experimentation can facilitate understanding of a multivariable object.

7. The multiplication device

7.1. Description of The Multiplication Device

The Multiplication Device realizes non-matrix “shape × color” logical multiplication (Fig. 6). The device has 2 rows of buttons located in a straight line. Each of the rows has 4 buttons. There are colored labels opposite the buttons of one row and labels with pictures of geometric forms opposite the buttons of the other row. The device also has 16 little round windows with electric lamps. The windows are integrated into 4 rows, each of the rows consisting of 4 windows. Each of the windows is characterized by two features, that is the color of the lamp and the form, or contour, circumscribed round the window. To light up a window one has to simultaneously press two buttons, one of which has a label of the same color and the other has a label with the same form. The technical properties of the device allow the experimenter to exchange positions of contours round the windows, as well as positions of the labels, and vary connections between the buttons and lamps thus producing different variants based on the general multiplication principle.

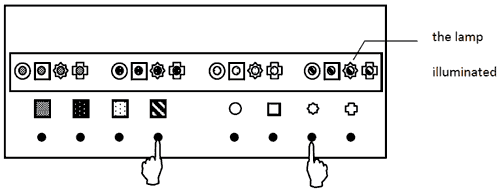
Figure 6. The Multiplication Device (top view)

7.2. Experiment: Transfer from the Multiplication Device to The Matrix Device and creating new knowledge

The Multiplication Device was used for training children and studying the opportunities of knowledge transfer to subsequent independent exploration of The Matrix Device. We supposed the trained children should be able to successfully explore the matrix device as a whole and, most importantly, to comprehend the subsystem which was not included into the content of the training (i.e., the subsystem of spatial relations of rectangular coordinates that was absent in The Multiplication Device).

Participants: 20 children of 5 years.

Procedure. The study was conducted in two stages. At the first stage the experimenter taught the children to use some techniques of combining actions and comprehending relations in The Multiplication Device. At the second stage of the study the children explored the control object (The Matrix Device) by themselves.

Results. For various subsystems of The Matrix Device, from 12 to 16 trained children (i.e., from 60% to 80%) showed a high level of control of the subsystems, including the subsystem of spatial relations that was not presented in the content of the previous teaching. Only one of 20 non-trained 5-year-olds could show a similar result. All the trained children performed the strategies of ordered combinatorial search that they learned while training, in particular, strategies of varying one button and keeping the other button constant. Only 4 non-trained children did so. (Differences between the trained and non-trained groups were significant at p<0.0125.) Thus, during independent experimentation on the novel multivariable object children aged 5 years could successfully transform the system of knowledge which had been given to them by the adult in the course of training. They transformed it into such a new system of knowledge that was adequate to the novel object and that was not in the content of the training.

8. Conclusion

1. Combinatorial (multivariable) experimentation aimed at exploration of multiple interactions in complex objects is a special aspect of children’s cognitive development. This activity can be very interesting for children and serve as a precondition for development of initial forms of system thought.
2. Most preschoolers can successfully combine actions, comprehend and use various multivariable objects containing hidden mechanical, logical and mathematical relationships (up to six variables), though their combinatorial strategies are not general and logically exact (are not of operational level, in Piaget’s terms).
3. One can distinguish between 4 stages of the combinatorial experimentation development in preschoolers: (a) pre-combinatorial; (b) systemic combining elements without organization of their interactions; (c) combining aimed at organization of interactions between elements and obtaining novel effects; (d) multilevel combinatorial experimentation (a child purposefully combines effects of interactions at lower levels to organize a complex interactive effect at higher levels–like in the experiments with The Mechanical Device).
4. The didactic objects can be considered as a means to identify and control the zone of a child’s proximal development, in Vygotskian terms. They are substitutes for an adult, helping the child to learn some activity independently. These objects are a means of dialogue between the cultures of adults and children: they reflect adults’ ideas about multivariable relations and scientific experimentation with them, ideas about children’s cognitive potentials and interests, and ideas about aims of the emerging dialogue itself.

The purpose of the toys described in this article is to stimulate the interest of a child, provoke them to “ask questions” to these objects, invent and test different hypotheses, elaborating their knowledge and competences. Experimenting on such objects, young children reach higher levels of cognitive achievements related to the development of causal thought and understanding of multivariable interactions, logical, physical and mathematical relationships.

References

Bruner, J.S. (1966). The process of education. Cambridge: Harvard University Press.

Demetriou, A., Efklides, A., Papadaki, M., Papantoniou, G., & Economou, A. (1993). Structure and development of causal-experimental thought: From early adolescence to youth. Developmental Psychology, 29(3), 480-497.

Dörner, D. (1997). The logic of failure: recognizing and avoiding error in complex situations. New York: A Merloyd Lawrence Book.

English, L.D. (1993). Children’s strategies for solving two and three-dimensional combinatorial problems. Journal for Research in Mathematics Education, 24(3), 255-273.

Flavell, J.H., Miller, P.H., & Miller, S.A. (2002). Cognitive development. Prentice Hall, NJ: Upper Saddle River.

Forman, G. (1986). Observations of young children solving problems with computers and robots. Journal of Research in Childhood Education, 1(2), 60-74.

Frensch, P.A., & Funke, J. (Eds). (1995). Complex problem solving: the European perspective. Hillsdale, NJ: Lawrence Erlbaum Associates.

Klahr, D., & Simon, H.A. (1999). Studies of scientific discovery: complementary approaches and convergent findings. Psychological Bulletin, 125(5), 524-543.

Poddiakov, A. (1992). Teaching preschoolers combinatory experimentation. Journal of Russian and East European Psychology, 30(5), 87-96.

Poddiakov, A. (1994). Preschoolers’ acquirement of competences in factor combining and factor interaction. In J. ter Laak, P.G. Heymans, & A.I. Podol’skij (Eds.), Developmental tasks (pp. 173-186). Dordrecht, Holland: Kluwer Academic Publishers.

Poddiakov, A. (2006). Issledovatel’skoe povedenie: strategii poznanija, pomosch, protivodejstvie, konflikt [Exploratory behavior: cognitive strategies, assistance, counteraction, and conflict]. Moscow: Erebus.

Poddiakov, N.N. (1995). Tvorchestvo i samorazvitie detej doshkol’nogo vozrasta: Konceptual’nyj aspekt [Creativity and self-development of preschool children: Conceptual aspect]. Volgograd: Peremena.

Schauble, L., & Glaser, R. (1990). Scientific thinking in children and adults. In Developmental perspectives in teaching and learning thinking skills (vol. 21, pp. 9-27). Basel: Karger.

Spector, M. (2005). Cognition and learning in the digital age: Promising research and practice. Paper presented at the International conference “Cognition and exploratory learning in digital age”. December 14-16, Porto, Portugal.

Strand-Cary, M., & Klahr, D. (2008). Developing elementary science skills: Instructional effectiveness and path independence. Cognitive Development, 23, 488-511.

Voss, H.-G. (2006). Exploratory learning in educational space: Some general considerations. Paper presented at the International conference “Exploratory activity of students”. November 23-24, Moscow, Russia.