Specific Features of the Relationships between Operational Structures within Preschoolers’ Systems of Thought
Abstract
Background. To build modern effective programs for the development of preschoolers’ logical thinking, it is necessary to study the specifics of the operational structures functioning within their thought systems. According to Piaget, two operational groups of thought develop in parallel and synchrony: 1) logical-mathematical (classification, seriation, and invariant construction — the conservation principle); and 2) spatial-temporal — the structuring of space (linear ordering [LO], transformation of geometric forms [TGS], reconstruction of sensorimotor space at the level of representations [RSMS]) and time. However, there has been no empirical verification of the significant links between the levels of development of an individual’s logical-mathematical and spatial-temporal operations in his/her system of thought.
Purpose. The purpose of this study was to examine the nature of the links between the elements of the logical-mathematical and spatial-operational structures in preschoolers’ systems of thought.
Design. The study involved the following steps: 1) Individual diagnosis of the developmental level of logical-mathematical and spatial operations in 52 preschool children (5,8 – 7,1 years) using classica Piaget techniques and the Bender-Gestalt test; 2) identification of the operational developmental stage of each examinee; and 3) identification of the nature of the links between the logical-mathematical and spatial operational structures within each child’s thinking system, using statistical tools for data analysis (ρ Spearman; regression analysis).
Results. Statistically significant differences between the developmental levels of spatial and logical-mathematical operations were revealed, as well as between the levels of development of spatial operations LO, TGS, and RSMS as measured by the Bender-Gestalt test. It was found that all the spatial operations (LO, TGS, RSMS) were conceived at a higher level than logical-mathematical operations (classification, seriation, and the conservation principle). Significant predictors of the development of logical-mathematical/spatial operations were identified.
Conclusions. Piaget’s hypothesis that the development of the logical-mathematical and spatial operations within a child’s thinking system is an interconnected process has received statistical justification in this study. The data we obtained suggest that both operational structures have similar sets of features. As proof that an internal causal nexus between the logical- mathematical and spatial structures exists, it is necessary to conduct formative experiments in which some thought operations (predictors) will be formed by training, while previously missing operations are induced to appear in the child’s thinking system indirectly.
Received: 14.06.2017
Accepted: 27.08.2018
Themes: Developmental psychology
PDF: http://psychologyinrussia.com/volumes/pdf/2018_3/psych_3_2018_13_Pogozhina.pdf
Pages: 183-194
DOI: 10.11621/pir.2018.0313
Keywords: logical thinking system, logical operations, spatial operations, preschoolers, Piaget
Introduction
Effective programs for developing preschoolers' logical thinking require new approaches, in light of increasing awareness of how mental processes are formed and develop. The modern stage of scientific development is characterized by a change of the rationality ideal in the sphere of scientific knowledge, as well as by a transition from non-classical models of knowledge to post-non-classical. Self-developing systems such as those of human beings and their activities, have become objects of knowledge (Mamardashvili, 2010; Stepin, 2012; Chernikova, 2011; Shvyrev, 2007, etc.). The mentality is seen as an open, nonlinear, non-equilibrium system (Prigogine, 1991; Klochko, 2008; Shabelnikov, 2013, etc.).
The functioning and development of nonlinear self-developing systems cannot be explained by external determinants alone. There is a so-called "actual start" within the system, which itself produces certain results, modifying the appearance and behavior of the system. Changes caused by external influences are not definitive, but probabilistic in nature, and identify the structure and characteristics of the system (Barybin, Korlyakov, 2011; Haken, 2015; Knyazeva, Kurdyumov, 2002; Nikolis, Prigogine, 1979; Prigogine, 1991; Prigogine, Stengers, 1986, etc.).
The nonlinearity, poly-variety, and instability of the dynamics of complex systems development require the examination of at least three groups of factors to be able to build developmental models of such systems, which can later become a basis for training program development. The three groups of factors include: 1) the system's own developmental trends (Group 1); 2) the methods of impact on the system (Group 2); and 3) external mechanisms of self-change processes initiated in the desired direction (Group 3) (Pogozhina, 2016). Therefore, in order to build modern, effective programs for aiding the development of preschoolers' logical thinking, it is necessary to study the specifics of the operational structures functioning within their thought systems (Group 1) (Pogozhina, 2015, 2016).
Piaget (1994) identifies two groups of operations in the preschoolers' thinking system: 1) the logical-mathematical, comprised of classification, seriation, and construction of an invariant (conservation principle) and 2) the spatial-temporal, comprised of three-dimensional design patterning (linear ordering, transformation of geometrical shapes, reconstruction of sensorimotor space at the level of representations), and the structuring of time (Piaget, 1994; Piaget, Inhelder, 2003; Bloom, Hastings, Madaus, 1971; Inhelder, Piaget, 2013; Piaget, Inhelder, Szeminska, 2013). These operations, especially the logical-mathematical, have been widely studied from the standpoint of their phenomenology, assessment diagnostic procedures development, and methods of formation. Examination of functional specifics, and the characteristics of the links between the levels of development of the various logical operations were carried out only within the logical-mathematical groups (Pogozhina, 2014, 2016; Astakhova Pogozhina, 2004; Pogozhina, 2011). Analysis of the links within the spatial-temporal operations group remained a challenge.
It should be noted that not all experts consider spatial operations to be part of a child's thinking system. Usually the child's spatial representations are studied based on Euclid's axiomatics (lines, squares, circles, angles, units, etc.). Empirical studies of perception confirm the existence of the child's spatial representations. From early childhood, the child forms a concept of space: the shape, the size, the ratio of figures and their elements in the space, objects localization, etc. (Bauer, 1985; Sergiyenko, 2006; Yakimanskaya 1980, etc.). However, analysis of geometric concepts shows that the child's initial spatial representations are not Euclidean, but "topological." That means that these representations are created only on the basis of qualitative ratios of double continuity, including such concepts as "connection and separation," "environment and order," etc., but excluding projectivity and distance conservation. According to Piaget and his colleagues, the children's spatial representations are topological in nature, and only later become simultaneously projective and Euclidean. In addition, these representations appear to be the result of motive activity and basic topological intuition (Piaget, 1994; Inhelder, Piaget, 2013; Piaget, Inhelder, Szeminska, 2013).
According to Piaget, from the child's point of view, at first there is no single space in which all objects and the child himself objectively (regardless of the child) exist. The child perceives a number of different spaces centered on his body. Gradually, during the child's development, these spaces begin to be coordinated, so that the child's spatial representations undergo significant changes. As a result, ideas appear about the constancy of objects existing independently of the child in a single space with him (the sensorimotor stage of intelligence development).
At the stage of concrete-operational thinking, the development of spatial representations continues. Projective and then metaphorical structures are formed on the basis of topological structures. Logical-mathematical and spatial structures are isomorphic towards each other. For example, the process of constructing an invariant (notions about conservation) is closely linked with the development of the ability to correlate various spatial parameters of objects among themselves (Piaget, 1994, p. 141–213, p. 594–628; Piaget, Inhelder, 2003; Piaget, Inhelder, Szeminska, 2013). If the child is perceiving logical-mathematical relationships between discontinuous, discrete objects of reality, then spatial operations "refer to the continuous objects and based on adjacency. These operations are built in parallel with the logical-arithmetic and in synchrony with them ... [emphasis added]" (Piaget, Inhelder, 2003, p. 105-106). However, there has been no empirical verification of the significance of the links between the levels of development of individual logicmathematical and spatial-temporal operations in a child's thinking system. Therefore studying them is still relevant.
Method
Goal [1]. Examination of the nature of the links between the elements of logicalmathematical and spatial operational structures in preschoolers' thinking systems.
Sample. 52 preschoolers aged five to seven years old (5,8 – 7,1) (N = 52). All participants were attending kindergartens, located in Moscow and Miass (Chelyabinsk region), Russia.
Diagnostic methods. 1) decentration assessment — a modified "Three Mountains" technique (Piaget, Inhelder, 2003, 2013; Pogozhina, Lyui, 2009); 2) logicalmathematical operations: classification, seriation, conservation (discrete numbers, length, volume) — Piaget methods (Piaget, 1994; Piaget, Inhelder, 2003; Bloom, Hastings, Madaus, 1971); 3) spatial linear ordering operations (LO), transformation of geometrical shapes (TGS) — Piaget methods (ibid. and Piaget, Inhelder, 2013); and 4) reconstruction of sensorimotor space at the level of representations (RSMS) — Piaget methods (ibid.), Bender-Gestalt test (Belopol'skii, Lovi, 2008). Classify levels (stages) of logical-mathematical and spatial operations development: I=operation is not formed; II=operation is partly formed; III=operation is formed in full.
Data statistical processing. SPSS 22.0 (ρ Spearman; regression analysis). Procedure. During individual classes which lasted from 30 to 50 minutes, the children performed diagnostic tasks in the following order: 1) the reconstruction of the sensorimotor space at the level of representations (Bender-Gestalt test); 2) decentration; 3) seriation; 4) classification; 5) understanding of the principle of conservation (discrete quantities, volume, length); 6) transformation of geometrical shapes; 7) linear ordering; and 8) reconstruction of the sensorimotor space at the level of representations (Piaget technique). Each examinee's level of operations development was identified on the basis of the diagnostic results. The data was the analyzed using statistical methods in order to identify the nature of the links between the logical-mathematical and spatial operational structures of the child's thinking system.
Results
Children's levels of operational structures development are formed inhomogeneously (see Figure 1).
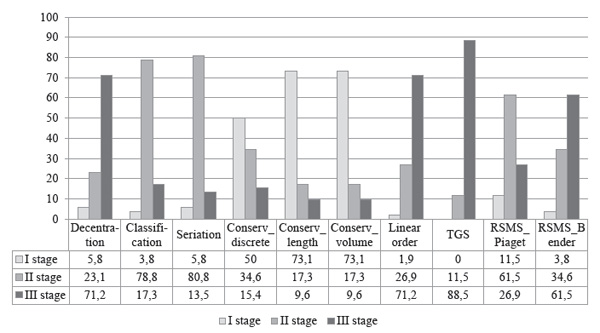
Figure 1. Levels of operational structures development (%; N = 52)
As seen in Figure 1, the ability to decentrate and carry out spatial operations is formed on a higher level than logical-mathematical group abilities. The data were processed using statistical analysis methods (ρ Spearman; regression analysis). Statistically significant differences between the developmental levels of logical-mathematical and spatial operations in the preschoolers' thinking systems were revealed (Table 1).
Table 1
Correlation ratios between operations within preschoolers' thinking systems (ρ Spearman; N = 52).
|
|
LO |
TGS |
RSMS_Piaget |
RSMS_Bender |
|
Decentration Piaget |
.053 |
.020 |
.008 |
-.154 |
|
Seriation |
.296* |
.333* |
.144 |
-.204 |
|
Classification |
.181 |
.361* |
-.040 |
-.051 |
|
Conservation_discrete |
.403** |
.092 |
.196 |
-.359** |
|
Conservation_length |
.105 |
.217 |
-.072 |
-.117 |
|
Conservation_volume |
.189 |
.217 |
.053 |
-.322* |
|
LO |
1,000 |
.290* |
.231 |
-.329* |
|
TGS |
.290* |
1,000 |
.269 |
-.317* |
|
RSMS Piaget |
.231 |
.269 |
1,000 |
-.525** |
|
RSMS Bender |
-.329* |
-.317* |
-.525** |
1,000 |
Note. ** Correlation is significant at 0.01 level (2-tailed). * Correlation is significant at 0.05 level (2-tailed).
As can be seen from Table 1, the level of LO spatial operations development is significantly positively associated with the developmental levels of logical-mathematical operations of seriation (p < 0.05) and discrete quantities conservation (p < 0.01). The level of TGS spatial operations development is significantly positively associated with the development levels of seriation (p < 0.05) and classification (p < 0.01). The level of RSMS spatial operations development, measured using Bender-Gestalt test, is significantly negatively associated with the levels of understanding of the discrete quantities conservation principle (p < 0.01) and the volume conservation principle (p < 0.05) (the negative relationship is determined by the Bender test scoring process: the lower the score, the higher the level of development of the RSMS).
Statistically significant differences within a group of spatial operations were also revealed (Table 1). There were relationships between the developmental levels of the LO and the TGS, and RSMS Bender (p < 0.05); between the TGS and RSMS Bender (p < 0.05) development levels; as well as between the RSMS developmental level measured by Piaget and the RSMS developmental level measured by the Bender-Gestalt test (p < 0.01).
The results of the regression analysis are presented in Table 2.
Table 2
Significant predictors for space operations (regression coefficients)
|
Linear order (LO) |
||||||||||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
||||||
|
В |
Std. Error |
Beta |
||||||||
|
(Constant) |
2,000 |
.334 |
|
5,991 |
.000 |
|||||
|
Seriation |
.333 |
.157 |
.287 |
2,118 |
.039 |
|||||
|
(Constant) |
2,248 |
.161 |
|
13,922 |
.000 |
|||||
|
Conservation of |
.269 |
.089 |
.392 |
3,009 |
.004 |
|||||
|
(Constant) |
3,138 |
.196 |
|
16,020 |
.000 |
|||||
|
RSMS_Bender |
-.010 |
.004 |
-.324 |
-2,423 |
.019 |
|||||
|
Transformation of geometrical shapes (TGS) |
||||||||||
|
(Constant) |
2,289 |
.207 |
|
11,072 |
.000 |
|||||
|
Classification |
.279 |
.095 |
.384 |
2,943 |
.005 |
|||||
|
(Constant) |
1,906 |
.258 |
|
7,379 |
.000 |
|||||
|
Seriation |
.217 |
.094 |
.293 |
2,312 |
.025 |
|||||
|
Classification |
.248 |
.092 |
.341 |
2,692 |
.010 |
|||||
|
Reconstruction of sensorimotor space at the level of representations (RSMS Bender) |
||||||||||
|
(Constant) |
58,569 |
5,529 |
|
10,593 |
.000 |
|||||
|
Conservation of |
-7,623 |
3,058 |
-.332 |
-2,493 |
.016 |
|||||
|
(Constant) |
56,873 |
5,231 |
|
10,871 |
.000 |
|||||
|
Conservation of |
-7,991 |
3,458 |
-.311 |
-2,311 |
.025 |
|||||
As can be seen from the Table 2, significant predictors for LO spatial operations are: seriation; understanding of the discrete quantities conservation principle; and reconstruction of the sensorimotor space at the level of representations (measured by Bender-Gestalt test) (p < 0.05; p < 0.01). The measure of understanding of the discrete quantities conservation principle more accurately predicts the possible level of LO operations development. For TGS spatial operations the following are meaningful predictors: classification; both classification and seriation; and reconstruction of the sensorimotor space at the level of representations (measured by methodology of Piaget) (p < 0.01; p < 0.05). The measure of classification and seriation predicts TGS development level more precisely. For RSMS spatial operations, measured by Bender-Gestalt test, predictors are the following: understanding of both the discrete and volume quantities conservation principles (p < 0.05). A negative coefficient means that children with higher levels of understanding the discrete and volume quantities conservation principle make fewer mistakes on the BenderGestalt test.
Discussion
Our data show that the operational structures within preschoolers' thinking systems are formed irregularly (Figure 1). The ability to decentrate and carry out spatial operations (LO, TGS, RSMS) is formed at a higher level than logical-mathematical operations (classification, seriation, and understanding the conservation principle). Within the spatial operations group, the best developed operation is the transformation of geometrical shapes (TGS): 88.5% of children scored at Stage III (the highest stage of development), and there was not one child (0%) who did not have this operation fully formed (i.e., was at the level of Stage I). Linear ordering (LO) also showed a high level of development: 71.2% of children have scored at Stage III, and only 1.9% of children at Stage I. Reconstruction of sensorimotor space at the level of representations, RSMS measured by Bender-Gestalt test, was fully formed (Stage III) in 61.5% of the children, and was not formed (Stage I) in only 3.8% of the children.
There is a discrepancy between the figures of the RSMS development level depending on whether the Piaget or Bender-Gestalt method was used. RSMS as measured by the Piaget technique was fully formed in only 26.9% of the children (Stage III), while 11.5% of the children did not have this operation fully formed (Stage I); the majority (61.5%) of the preschoolers was at Stage II. (Figure 1). From our point of view, such a discrepancy is caused by the fact that the Bender-Gestalt test has clearer and more formalized evaluation criteria than Piaget's methodology. Therefore the Bender-Gestalt test provides more precise data on the level of development. Both methods measure the performance of the same spatial operations and show a significant correlation (ρ Spearman; p<0.01) (Table 1). From our point of view, the RSMS indicators obtained by the Bender-Gestalt test are more precise, a finding which is confirmed by its coherence with other developmental indicators of the spatial operations group (LO and TGS) (Figure 1, Table 1).
Spatial decentration ability is as highly developed as spatial operations. 71.2% of the children scored at Stage III, and only 5.8% of the preschoolers at Stage I. However, there are no significant relationships between the developmental levels of the decentration ability and spatial operations (Table 1). These results are not really consistent with Piaget's beliefs about the place of decentration in a child's thinking system and its impact on the process of building operational structures (Inhelder, Piaget, 2013; Piaget, Inhelder, 2003). Therefore these data require further empirical validation and analysis. Perhaps the lack of a meaningful relationship is associated with significant differences in the content of the data on thinking structures.
The level of development of the logical-mathematical group's operations was lower than spatial group's operations. Seriation and classification operations were mostly at Stage II of development (80.8% and 78.8% respectively). Understanding of the discrete quantities, length, and volume conservation principle was at Stage I (50%; 73.1%; 73.1% respectively). This result may indicate that logical operations of classification and seriation are formed in children faster than understanding of the conservation principle. The data is consistent with Piaget's views about the relationship between the levels of development of logical-mathematical operations (Piaget, 1994; Piaget, Inhelder, 2003), and are consistent with the results of our previous research (Pogozhina, 2014, 2016).
Comparison of the developmental levels of logical-mathematical and spatial operations within the children's thinking systems suggests that spatial operations are formed earlier, and may have some impact on the development of other elements of the system–in particular, on the logical-mathematical operations group. Our research on the logical-mathematical operations group (classification, seriation, conservation) and decentration has experimentally confirmed that it is possible to form and develop operational structures as complex self-organizing systems through already existing content within the child's cognitive system, by external initiation (external cause) of content which stimulates self-organization mechanisms (internal cause). This increases the child's developmental level as a whole from the pre-operational level to the concrete-operational level (Pogozhina, 2014, 2016; Pogozhina, Lyui, 2009).
As much as that is true for the logical-mathematical operations group, we suggest that increased levels of development of spatial operations by managed learning can be an external cause for initiating self-change processes of logical-mathematical content within the child's thinking system. This will open up a new way of building modern efficient programs for developing preschoolers' cognitive structures. Nevertheless, in order to test this hypothesis, it is necessary to identify significant relationships between the developmental levels of spatial and logical-mathematical operations (Pogozhina, 2015).
Statistical methods of data analysis (ρ Spearman) revealed significant relationships between some logical-mathematical and spatial operational structures (Table 1). Such relationships were revealed between seriation, the discrete quantities conservation principle, and linear ordering (LO); between classification, seriation, and the transformation of geometrical shapes (TGS); and between the conservation of discrete quantities, volume, and space on the first (RSMS Bender). Relationships were also revealed between all elements within the spatial operations group (LO, TGS, RSMS); that is consistent with the views of Piaget on the relationship between operational structures and their mutual influence (Piaget, 1994). This relationship also corresponds with the available data on the existence of significant positive relationships between the structures within the logical-mathematical operations group (Pogozhina, 2015b).
There is no significant relationship between the ability to decentrate and spatial operations development. In our opinion this can be explained by the fact that decentration requires the development of a much higher degree of abstract thinking than other spatial operations. Decentration also illustrates a higher level of development of the child's operational thinking system. Therefore we concede that decentration is not associated with the formation of spatial operations at a certain stage of a child's mental development.
Regression models, along with the correlations, are of great interest in interpreting our results (Table 2). Regression analysis showed that the most significant predictors of LO operations were the development of understanding the principle of discrete quantities conservation (p < 0.01) and seriation (p < 0.05). In the case of TGS, the predictors were classification (p < 0.01), and both classification and seriation together (p < 0.05). In the case of RSMS, the predictors were the discrete quantities conservation principle (p < 0.05) and the volume conservation principle (p < 0.05).
Linear regression analysis also showed that there could be reverse dependencies. These results are consistent with the theoretical assumptions of Piaget, who believed that the genesis of space in sensorimotor intelligence is subject to motions development. The structure of such movements is developed gradually and as a result reaches an equilibrium motor organization state, the structure of the "group."
Equilibrium of structural components requires reversibility and identity. However, reversibility and identity, along with other conditions (combinativity, associativity, tautology), provide a balance between of basic groups (including classification and seriation logical operations). The emergence groups, in turn, is connected with the construction of invariants, i.e. concepts conservation (Piaget, 1994; Piaget, Inhelder, 2003). This explains the significant relationship between the developmental levels of logical-mathematical and spatial operations. After all, reversibility and identity are included in both spatial and logical-mathematical operations.
As a result of our empirical research, we found that the operational structures of preschoolers' thinking systems operate and develop in an interconnected manner, so that an increase of the developmental level of some system operations is accompanied by an increase of the developmental level of other operations. We therefore conclude:
-
There is a significant relationship between the developmental levels of spatial and logical-mathematical operations, namely:
- between the developmental levels of the linear ordering spatial operations (LO) and logical-mathematical operations group–seriation (p<0.05), and the discrete the quantities conservation principle (p < 0.01);
- between the developmental levels of the transformation of geometrical shapes (TGS), and seriation (p < 0.05) and classification (p < 0.01);
- between the developmental levels of reconstruction of sensorimotor space at the representational level, measured by Bender-Gestalt test (RSMS Bender), understanding of the discrete quantities conservation principle (p < 0.01), and understanding the volume conservation principle (p < 0.05);
-
There is a significant relationship between the developmental levels of linear ordering spatial operations (LO), transformation of geometrical shapes (TGS), and reconstruction of sensorimotor space at the level of representations (RSMS Bender) (p < 0.01; p < 0.05).
-
-
Spatial group operations (LO, TGS, RSMS) are formed at a higher level than logical-mathematical operations (classification, seriation, understanding the principle of conservation). Significant predictors of the development of logicalmathematical/ spatial operations were identified (regression analysis). Significant predictors of logical-mathematical operations development are the following spatial operations:
- Spatial operation LO is a predictor for the logical operation of seriation (p < 0.05). Thus, preschoolers who properly perform the task on the linear ordering have a higher development level of seriation and vice versa;
- Spatial operation TGS is a predictor for the logical-mathematical operation of classification (p < 0.01), as well as classification and seriation together (p < 0.05). This means that these operations contribute to the development of each other.
- Spatial operation LO is a predictor of the understanding of the principle of discrete quantities conservation (p < 0.01) and RSMS Bender (p < 0.05). This means that children who make fewer mistakes in linear ordering tasks and Bender-Gestalt test tasks, have a higher level of understanding of the conservation principle, and vice versa;
- The RSMS Bender spatial operation is a predictor of the understanding of the volume conservation principle (p < 0.05). This means that RSMS operations and understanding the conservation principle contribute to maintaining each other's level of development.
-
Spatial group operations (LO, TGS, RSMS) are formed at a higher level than logical-mathematical operations (classification, seriation, understanding the principle of conservation). Significant predictors of the development of logicalmathematical/ spatial operations were identified (regression analysis). Significant predictors of logical-mathematical operations development are the following spatial operations:
-
The significant relationships we identified between logical-mathematical and spatial operations in preschoolers' thinking systems cannot be regarded as proof of a causal relationship between them. However, the data suggest that the operational structures we studied have a similar set of components, and that is why the appearance of new content in the subject's operational system, and its inclusion in an operational structure, increases the level of its development.
-
In order to prove the existence of internal causal dependencies between the structures of the logical-mathematical and spatial operational systems, it is necessary to conduct formative experiments in which some operations (predictors) will be formed by a managed learning process, while other previously missing operations will appear indirectly through the formation of the mentioned operations.
References
Astakhova, I.V. & Pogozhina, I.N. (2003) O vzaimosvyazi urovnei razvitiya logicheskikh operatsii klassifikatsii, seriatsii i sokhraneniya u detei doshkol'nogo vozrasta [On the relationship between the development levels of classification, seriation logical operations and conservation in preschool children]. Vestnik Moskovskogo universiteta. Ser. 14, Psikhologiya [Moscow University Psychology Bulletin. Series 14. Psychology], 3, 52-61.
Barybin, A.A. & Korlyakov, A.V. (2011). Neravnovesnaya termodinamika [Non-equilibrium thermodynamics]. Saint-Petersburg: Publ. GETU LETI, 2011.
Belopol'skii, V.I. & Lovi, O.V. (2008). Zritel'no-motornyi Bender geshtal't-test [Bender VisualMotor Gestalt Test]. Moscow: Kogito-Tsentr.
Bloom, B.S., Hastings, J.T., & Madaus, G.F. (1971). Handbook on formative and summative evaluation of student learning. Ch. 13. New York: McGraw-Hill. Bower, T.G.R. (1985). Psikhicheskoe razvitie mladentsa [Development in infancy]. Moscow: Progress.
Chernikova, I.V. (2011). Tipologiya nauki v kontekste sovremennoi filosofii nauki [Typology of science in the context of contemporary philosophy of science]. Voprosy filosofii [Issues of philosophy], 11, 71-78.
Haken, H. (2015). Sinergetika. Printsipy i osnovy. Perspektivy i prilozheniya [Synergetics: Introduction and Advanced Topics. Perspectives and applications]. Moscow: URSS: LENAND.
Klochko, V.E. (2008) Postneklassicheskaya nauka i problema ob"yasneniya v psikhologii [Postnonclassical science and the problem of explanation in psychology]. Metodologiya i istoriya psikhologii [Methodology and History of Psychology], 3, (1), 165-178.
Knyazeva, E.N. & Kurdyumov, S.P. (1992) Sinergetika kak novoe mirovidenie: dialog s I.Prigozhinym [Synergetics as a new vision of the world: dialogue with I. Prigogine]. Voprosy Filosofii [Issues of philosophy], 12, 3-20.
Mamardashvili, M.K. (2010). Klassicheskii i neklassicheskii idealy ratsional'nosti [Classical and non-classical ideals of rationality]. Saint-Petersburg: Pabl. Azbuka.
Nikolis, G., & Prigozhine, I. (1979). Samoorganizatsiya v neravnovesnykh sistemakh: Ot dissipativnykh struktur k uporyadochennosti cherez fluktuatsii [Self-organization in non-equilibrium systems: From dissipative structures for ordering through fluctuations]. Moscow: Mir.
Piaget, J. & Inhelder, B. (2003). Psikhologiya rebenka [La psychologie de l'enfant]. 18en ed. St. Petersburg: Piter.
Piaget, J. (1994). Izbrannye psikhologicheskie trudy [Selected Psychological Works]. Moscow: International Pedagogical Academy.
Piaget, J. & Inhelder, B. (2013). The child's conception of space. London, New York: Routledge.
Piaget, J., Inhelder, B., & Szeminska, A. (2013). Child's Conception of Geometry. London, New York: Routledge.
Pogozhina, I. (2014). Development of the logical operations in preschool children. Procedia Social and Behavioral Sciences, 146, 290-295. https://doi.org/10.1016/j.sbspro.2014.08.132
Pogozhina, I. (2016b) Comparative study of the degree of the relationship between the logical thinking operational structures development levels in preschoolers from Russia and China. Procedia Social and Behavioral Sciences, 233, 492-497. https://doi.org/10.1016/j. sbspro.2016.10.201
Pogozhina, I.N. (2011). Detsentratsiya u doshkol'nikov: empiricheskii analiz fenomena, ili chto na samom dele diagnostiruyut metodiki Kh'yuza i Piazhe [Decentration in preschool children: An empirical analysis of the phenomenon or what is actually diagnosed by Hughes and Piaget's methods]. Vestnik Moskovskogo universiteta. Seriya 14. Psikhologiya [Moscow University Psychology Bulletin. Series 14. Psychology], 3, 132-143.
Pogozhina, I.N. (2015). Determinatsiya razvitiya struktur logicheskogo myshleniya skvoz' prizmu postneklassicheskoi paradigmy [Determination of logical thinking through the prism of the postnonclassical paradigm]. Natsional'nyi psikhologicheskii zhurnal [National Psychological Journal], 3(19), 35-44. https://doi.org/10.11621/npj.2015.0304
Pogozhina, I.N. (2015b). Issledovanie kharaktera vzaimosvyazei mezhdu urovnyami razvitiya operatsional'nykh struktur sistemy logicheskogo myshleniya pri perekhode ot dooperatsional'nogo k konkretno-operatsional'nomu etapu razvitiya [A study of the nature of the relationships between the operational structures levels of logical thinking under transfer from the preoperational stage of thinking development to the concrete-operational]. Psikhologicheskie Issledovaniya [Psychological Studies], 8(44), 8. Retrieved from http:// psystudy.ru/index.php/num/2015v8n44/1212-pogozhina44.html
Pogozhina, I.N. (2016). Formirovanie i razvitie poznavatel'nykh struktur: determinanty i mekhanizmy. Postneklassicheskaya model'. Monografiya [Formation and development of cognitive structures: determinants and mechanisms. Post-nonclassical model. Monograph]. Moscow: NIYaU MIFI.
Pogozhina, I.N. & Lyui, G. (2009). Vliyanie umeniya detsentrirovat'sya na uroven' sformirovannosti konkretno-operatsional'nykh struktur u starshikh doshkol'nikov [Influence of the decentration ability on the level of concrete-operational structure formation at the senior preschool children]. Vestnik Moskovskogo universiteta. Ser. 14, Psikhologiya [Moscow University Psychology Bulletin. Series 14. Psychology], 2, 45-55.
Prigogine, I. (1991). Filosofiya nestabil'nosti [Instability Philosophy]. Voprosy filosofii [Issues of philosophy], 6, 46-57.
Prigogine, I. & Stengers, I. (1986). Poryadok iz khaosa. Novyi dialog cheloveka s prirodoi [Order out of chaos: Man's new dialogue with nature]. Moscow: Progress. Sergienko, E.A. (2006). Rannee kognitivnoe razvitie. Novyi vzglyad [Early cognitive development. A New Look]. Moscow: IPRAN.
Shabel'nikov, V.K. (2013). Funktsional'naya psikhologiya. Formirovanie psikhologicheskikh system [Functional psychology. Formation of psychological systems]. Moscow: Akademicheskii proekt; Kul'tura.
Shvyrev, V.S. (2007). O sootnoshenii poznavatel'noi i proektno-konstruktivnoi funktsii v klassicheskoi i sovremennoi nauke [On the relationship between cognitive and structural design and functions in classical and modern science]. In V.A. Lektorskii (Ed.), Poznanie, ponimanie, konstruirovanie [Knowledge, understanding, designing] (pp. 30-47). Moscow: IFRAN.
Stepin, V.S. (2012). Nauchnaya ratsional'nost' v tekhnogennoi kul'ture: tipy i istoricheskaya evolyutsiya [Scientific rationality in technogenic culture: types and historical evolution]. Voprosy filosofii [Issues of philosophy], 5, 18-25.
Yakimanskaya, I.S. (1980). Razvitie prostranstvennogo myshleniya shkol'nikov [Development of schoolchildren's spatial thinking]. Moscow: Prosveshchenie.
Notes
1. The research was carried out by us and under our supervision in collaboration with V.A. Kislova within her degree work.
To cite this article: Pogozhina I.N. (2018) Specific Features of the Relationships between Operational Structures within Preschoolers’ Systems of Thought. Psychology in Russia: State of the Art, 11 (3), 183-194
The journal content is licensed with CC BY-NC “Attribution-NonCommercial” Creative Commons license.









