The Factorial Structure of Spatial Abilities in Russian and Chinese Students
Abstract
Background. Recent research has suggested a unifactorial structure of spatial ability (SA). However, further studies are needed to replicate this finding in different populations.
Objective. is study aims to explore the factorial structure of SA in samples of 921 Russian and 229 Chinese university students.
Design. A gamified spatial abilities battery was administered to all participants. e battery consists of 10 different domains of SA, including 2D and 3D visualization, mental rotation, spatial pattern assembly, spatial relations, spatial planning, mechanical reasoning, spatial orientation, and spatial decision-making speed and flexibility.
Results. The results of the factor analysis showed a somewhat different pattern for different samples. In the Russian sample, the unifactorial structure, shown previously in a large UK sample (Rimfeld et al., 2017), was replicated. A single factor explained 40% of the variance. In the Chinese sample two factors emerged: the first factor explained 26% of the variance and the second factor, including only mechanical reasoning and cross-sections tests, explained 14%. e results also showed that the Chinese sample significantly outperformed the Russian sample in five out of the 10 tests. Russian students showed better performance in only two of the tests. The effects of all group comparisons were small.
Conclusion. Overall, a similar amount of variance in the 10 tests was explained in the two samples, replicating results from the UK sample. Future research is needed to explain the observed differences in the structure of SA.
Received: 03.08.2018
Accepted: 14.10.2018
Themes: Educational psychology; Developmental psychology
PDF: http://psychologyinrussia.com/volumes/pdf/2018_4/psych_4_2018_7_likhanov.pdf
Pages: 96-114
DOI: 10.11621/pir.2018.0407
Keywords: spatial ability (SA), factorial structure, Russian and Chinese students
Introduction
Spatial ability (SA), “the ability to generate, retain, retrieve, and transform well-structured visual images” (Lohman, 1996), has been extensively studied for the last 60 years (Kell & Lubinski, 2013). However, it is still not clear whether spatial ability is a unitary construct or whether it has a more complex structure (Aristova et al., 2018). The results of psychometric studies suggest several components of spatial abilities: spatial visualization (Lohman, 1979), spatial orientation (Hegarty Montello, Richardson, Ishikawa, & Lovelace 2006), spatial imagination (Jansen, 2009), mental rotation (Shepard & Metzler, 1971) and spatial relations (Lohman et al., 1987). Researchers have also suggested different classifications for the numerous components of spatial ability. For example, Uttal and colleagues (2013) suggested a classification based on the combination of intrinsic/extrinsic and static/dynamic categories of spatial skills.
Nevertheless, most studies of SA components have suggested the existence of two groups of components: small- and large-scale spatial abilities (Jansen, 2009). The small-scale group includes spatial visualization, spatial imagination, and mental rotation (Jansen, 2009). These abilities involve mental operations with objects: transformation (Zacks, Mires, Tversky, & Hazeltine, 2000), mental rotation (Blajenkova & Kozhevnikov, 2005), and manipulation (Kozhevnikov & Hegarty, 2001). The large-scale group includes spatial orientation; object location from the spectator’s point of view and an ability to assess the direction and distance (Jansen, 2009); navigation ability (Kozhevnikov, Motes, Rasch, & Blajenkova 2006); sense of direction (DeBeni & Pazzaglia, 2006), spatial orientation (Kozhevnikov & Hegarty, 2001); and other abilities. This group of abilities is connected with changes in the spectator’s visual perspective, while other objects’ positions remain the same (Hegarty & Waller, 2004).
It is unclear whether small- and large-scale skills are independent or a part of a unitary meta-construct. Hegarty and colleagues (2006) discussed four models which purport to explain the relationships between these two types of skills:
- the “unitary model” assumes that both skills overlap completely;
- the “total dissociation model” assumes that the skills are distinct;
- the “partial dissociation model” assumes that the abilities have similarities and differences;
- and the “mediation model” assumes that small- and large-scale skill are linked, but this link is mediated by a third variable (i.e., intelligence).
The results of meta-analysis of psychometric studies from 1985 to 2014 (Wang et al., 2014) confirmed the dissociation between small- and large-scale abilities, with only a moderate correlation (r=.27) between them. Neuropsychological studies also suggest a partial dissociation between small- and large-scale spatial abilities (Hegarty et al., 2006; Morris & Parslow, 2004). Small-scale spatial ability tasks are associated with the parietal lobes (Kosslyn & Thompson, 2003), whereas large-scale spatial abilities have been linked to the hippocampus (Gogos et al., 2010; Hughdahl et al., 2006) and medial and temporal lobes (Parslow et al., 2004). There are also activation patterns triggered by both groups of tests such as, for example, vision, muscle sense, etc. (Wang, 2014).
Experimental studies further support the partial dissociation model. For example, one study (Jansen, Wiedenbauer, & Hahn, 2010), conducted in adults, showed that large-scale ability can be improved slightly by training which uses small-scale ability tasks (ή2=.12). However, there was no such effect in another study with the same design, but which involved children (Jansen, 2009). Given these results, a partial dissociation model seems rather plausible, suggesting that small- and large-scale skills can be studied separately. In the present paper, we focus on the structure of SA related to small-scale skills.
Research that attempts to clarify the structure of SA requires administration of a large number of tests, which makes it difficult in practice. One way to reduce the strain on participants during such studies is to use gamified online testing. A recent study by Rimfeld and colleagues (2017) introduced a gamified online spatial abilities battery (King’s Challenge), which assesses 10 different small-scale spatial ability domains: 1) mazes task (searching for a way through a 2D maze in a speeded task); 2) 2D drawing (sketching a 2D layout of a 3D object from a specified viewpoint); 3) Elithorn maze (joining together as many dots as possible from an array); 4) pattern assembly (visually combining pieces of objects together to make a whole); 5) mechanical reasoning (multiple-choice naïve physics questions); 6) paper folding (visualizing where the holes are situated after a piece of paper is folded and a hole is punched through it); 7) 3D drawing (sketching a 3D drawing from a 2D diagram); 8) shape rotation (mentally rotating objects); 9) perspective-taking (visualizing objects from a different perspective); and 10) cross-sections (visualizing cross-sections of objects).
The study was conducted on 1367 twin pairs (ages 19–21) from the UK-representative Twins Early Development Study (TEDS). The results of the study suggested a unifactorial structure of small-scale SA. Factor loadings ranged from .44 to .71 for different tests, with perspective-taking and mazes having the lowest loadings, and 3D drawing having the highest (see Fig. 2 in Rimfeld et al., 2017). The study also showed that individual differences in this construct were largely explained by genetic factors (69%).
More research is needed in order to test whether this unitary structure of SA can be replicated in different cultures. Cross-cultural comparison of the structure of SA may be useful for understanding the sources of individual differences within any population. A study by Sakamoto and colleagues (2014) showed that Chinese and Japanese adults on average demonstrate greater visual spatial ability than U.S. adults (Cohen’s d=0.5-0.7). This advantage may be explained by the impact of the Chinese writing system on the development of spatial ability (Flaherty & Connolly, 1995; Gitterman & Sies, 1992; Rodic et al., 2015), or by other cultural differences
In the present study we aim to replicate the unitary structure which was suggested by Rimfeld and colleagues (2017), using an adaptation of the same King’s Challenge battery, in Russian and Chinese samples. The main aims of the study were: 1) to explore the factorial structure of SA in the two student samples: Russian and Chinese; 2) to compare the factorial structures in both samples with the previously reported findings from the UK population; and 3) to evaluate the relative strengths and weaknesses in performance on the 10 tests, across the two samples.
Methods
Participants
The sample consisted of students from Russia and China.
The Russian sample consisted of 921 participants (16 to 37 years old, M=19.59, SD=1.85; 348 males and 573 females). Participants were recruited from five leading universities in Russia: three universities from the top 10, and two from the top 100, out of the more than 500 universities in Russia.
The Chinese sample consisted of 229 participants (17 to 30 years old, M=19.92, SD=1.73; 88 males and 114 females). Participants were recruited from top-tier universities: one university from top 15-20, and one university from the top three to five, out of the approximately 300 universities in China. The initial sample included 245 students, but data from 16 participants were excluded because of reported technical problems.
Reference Sample
The current study aims to replicate the factorial structure of SA, previously shown in the UK sample using the same 10-measure instrument. Therefore, we compare our results to the reference sample, the Twin Early Development Study (TEDS; Rimfeld et al., 2017). The TEDS is an unselected sample, representative of the UK population. The results reported in Rimfeld et al. are not directly comparable to the student samples collected in the present study. We conducted additional analyses on the TEDS data, selecting only participants who reported being involved in higher education. Unlike the students in the present study, who came from top universities, the TEDS students were undergraduate and postgraduate students from a large number of unselected universities in the UK and abroad. For this reason, we do not directly compare the results with the UK student sample. In terms of the structure of SA, the results (available from the authors) showed a very similar structure for the TEDS student subsample as for the whole UK sample. Therefore, we compare our results with the results published in Rimfeld et al. (2017).
Measures
Spatial Ability
All participants completed interactive tests from the King’s Challenge (KC) gamified interactive battery, translated into Russian and Chinese. As described in the introduction, KC is an online battery that tests 10 major dimensions of spatial ability: mental rotation, spatial visualization, spatial reasoning, perspective-taking, and mechanical reasoning (see Esipenko et al., this issue for more detail on each test). The battery is gamified, so that participants engage in building and protecting the King’s Castle, with all tests linked by the same storyline. The total score was computed by summing the results from all 10 tests. Each of the 10 tests included a different number of items, and presented different levels of difficulty (see Esipenko et al., this issue).
Demographic information
Demographic information, including age, sex, and level of education, was collected in both samples, using an online questionnaire.
Procedure
The data for the Russian sample were collected in one session at the participants' universities.
The Chinese participants were recruited by emailing participants and inviting them to complete the on-line test battery. Data from respondents who experienced technical issues in any test were excluded from the analyses.
Results
Descriptive statistics
Table 1 presents the means, standard deviations, standard error, and split-half reliability for the 10 spatial measures for Russian and Chinese samples. Differences in the number of participants across the tests is explained by some respondents not completing the whole battery. According to the criteria suggested by Comrey and Lee (1992), the sample size was adequate (Chinese sample) and excellent (Russian sample) for the performed analyses. See density plots for all variables for both Russian and Chinese samples in Appendix, Figures 1, 2.
Table 1. Descriptive statistics for KC tests
|
|
Russia |
China |
||||
|
|
n |
Split-half |
mean (SD) |
mean (SD) |
Split-half |
n |
|
Cross-sections |
921 |
.74 |
6.71 (3.65) |
8.06 (3.74) |
.82 |
229 |
|
2D drawing |
918 |
.80 |
3.53 (1.23) |
3.63 (1.19) |
.80 |
229 |
|
Pattern assembly |
909 |
.69 |
6.37 (3.04) |
7.37 (3.10) |
.74 |
229 |
|
Elithorn maze |
904 |
.88 |
7.74 (1.97) |
6.99 (2.15) |
.90 |
227 |
|
Mechanical reasoning |
902 |
.56 |
9.76 (2.70) |
10.75 (2.43) |
.54 |
225 |
|
Paper folding |
897 |
.85 |
8.17 (4.25) |
10.55 (3.54) |
.83 |
224 |
|
3D drawing |
889 |
.78 |
2.52 (1.82) |
2.87 (1.80) |
.93 |
224 |
|
Shape rotation |
886 |
.82 |
7.76 (4.05) |
8.82 (3.71) |
.79 |
223 |
|
Perspective taking |
885 |
.86 |
4.45 (4.14) |
3.29 (3.07) |
.80 |
223 |
|
Mazes |
883 |
.60 |
5.35 (2.03) |
5.47 (2.06) |
.63 |
222 |
|
Total score |
883 |
NA |
62.40 (19.66) |
68.24 (17.94) |
NA |
222 |
Note. The results of the different subtests cannot be directly compared, as they each included a different number of items.
Given the consistent sex differences reported for spatial ability (see, for example, Tosto et al., 2014; Toivainen et al., 2018), sex differences in the Chinese and Russian samples were examined before factor analysis was done. In the Russian sample, males outperformed females on all tests, with ή2 ranging from 1% to 11% (see Esipenko et al., in this issue for more information). In the Chinese sample, significant sex differences were present for only three out of 10 tests: cross-sections (7%), mechanical reasoning (5%), and mazes (10%). In these tests, males outperformed females: cross-sections (9.69 vs. 7.95); mechanical reasoning (11.45 vs. 10.48); and mazes (6.30 vs 5.16), with Cohen’s d ranging from 0.47 to 0.67.
Therefore, for further analysis, sex differences were regressed out from all tests for the Russian sample, and from the three tests for the Chinese sample.
Correlational analysis
First, we performed a Pearson’s correlation analysis for the 10 King’s Challenge tests, in both the Russian and Chinese samples. All correlations were positive, ranging from r=.15 to r=.80, and were significant after Bonferroni correction for multiple comparisons. The Elithorn maze and mazes tests were the least associated with the other tests (as well as to the total score). The exact correlation coefficients can be found in Appendix, Table 1 (for the Russian sample) and Appendix Table 2 (for the Chinese sample).
Factor analysis
Our main aim was to replicate the unifactorial structure reported by Rimfeld et al. (2017) in the unselected UK sample. We first examined the factorability of the 10 tests in the Russian sample. Several well-recognized criteria for the factorability of a factor analysis were used. First, it was observed that 10 out of 10 tests correlated at least .3 with at least one other test, suggesting reasonable factorability (see Appendix, Table 1). Secondly, the Kaiser-Meyer-Olkin measure of sampling adequacy turned out to be .93 (above the commonly recommended value of .6; Cerny & Kaiser, 1977); and Bartlett’s test of sphericity was significant (χ2 (45)=2881.98, p<.0001). The diagonals of the anti-image correlation matrix were also all over .9. Finally, with the exception of the Elithorn maze, the communalities were all above .3 (see Appendix, Table 3), further confirming that each test shared some common variance with other tests. Given these overall indicators, factor analysis was deemed to be suitable for all 10 tests.
The PCA scree plot (see Appendix, Figure 3) and eigenvalues suggested single factor extraction (eigenvalue equals 4.59). Initial eigenvalues suggested that this factor explained 45.94 percent of the variance. Finally, the Root Mean Square Error of Approximation (RMSEA) of .03 (min=.017, max=.041, CI=.9), the Tucker Lewis Index (TLI) of .983, and the Comparative Fit Index (CFI) of .988 were also consistent with the single factor model. Confirmatory factor analysis showed that factor loadings ranged between .44 (for Elithorn’s maze) to .76 (3D drawing), totally accounting for 40% of the overall variation (see Table 2 for details on factor loadings). These results are consistent with the results from the unselected UK sample, where 42% of the overall variance was explained.
Table 2. Factor loadings for the King’s Challenge subtests for both samples.
|
|
Russian sample |
Chinese sample |
|
|
Subtest name |
Factor 1 |
Factor 1 |
Factor 2 |
|
Cross-sections |
.65 |
.03 |
.68 |
|
2D drawing |
.73 |
.57 |
.14 |
|
Pattern assembly |
.56 |
.35 |
.23 |
|
Elithorn maze |
.44 |
.64 |
-.05 |
|
Mechanical reasoning |
.65 |
.02 |
.64 |
|
Paper folding |
.71 |
.54 |
.29 |
|
3D drawing |
.76 |
.53 |
.26 |
|
Shape rotation |
.66 |
.74 |
-.09 |
|
Perspective taking |
.55 |
.25 |
.15 |
|
Mazes |
.52 |
.60 |
-.14 |
|
Variance explained by a factor |
40% |
26% |
14% |
|
Cumulative variance |
40% |
40% |
|
In the Chinese sample, eight of the 10 tests correlated at least .3 with at least one other test, suggesting reasonable factorability (see Appendix, Table 2). The Kaiser-Meyer-Olkin measure of sampling adequacy was .82, and Bartlett’s test of sphericity was significant (χ2 (45)=313.71, p<.001). The diagonals of the anti-image correlation matrix were also all over .75. Finally, with the exception of pattern assembly and perspective-taking, the communalities were all above .3, further confirming that the tests shared some common variance with other tests (see Appendix Table 3). Given these overall indicators, factor analysis was deemed to be suitable for all 10 tests. Pattern assembly and perspective-taking were also added to the analysis to enable factor structure comparisons across the samples.
In the Chinese sample, scree plot and eigenvalues (3.35 and 1.19 for the first and second factor, respectively) suggested a two-factor structure of the data (see Appendix, Figure 4). The first two factors explained 33.5 and 11.9 percent of variance, respectively. Only two tests (cross-sections and mechanical reasoning) mostly loaded on the second factor. Oblimin rotation was used in principal component analysis, because the correlation between factors was .3. Moreover, without rotation, there were several tests which demonstrated cross-loadings of more than .4 to both factors. After rotation was applied, cross-loadings decreased to the level of .3, which clarified the relationships between the clusters of tests.
Confirmatory factor analysis also supported the two-factor model of SA in the Chinese sample. The RMSEA of a single-factor extraction was too high (.064, with min= .039, max=.086, CI=0.9); while the two-factor model (the one with cross-sections and mechanical reasoning as a second factor) score for RMSEA was .037 (min=0, max=.067, CI=0.9). Also, ANOVA showed significant differences between the fit for the unifactorial and two-factorial models (χ2=10.85, p<.001), with the two-factor model showing a better fit (χ2=39.99) than the unifactorial model (χ2 diff = 50.85). Confirmatory factor analysis showed that the two-factor solution explained 40% of the overall variance, factor loadings are presented in Table 2.
Means comparison
The performance levels for the two samples were compared using t-tests, implementing the FDR correction for multiple comparisons (See Appendix, Table 4). As can be seen from Figure 1, the Russian and Chinese samples significantly differed in the total score and individual tests, with the exception of 2D drawing, 3D drawing, and mazes. The Chinese students on average outperformed Russian students on five tests (with Cohen’s d ranging from .27 to .58, p< .001). The Russian students outperformed the Chinese sample on the Elithorn maze and perspective-taking (Cohen’s d was .30 and .37 for perspective-taking and Elithorn maze, respectively; p<.001) (see Figure 1).
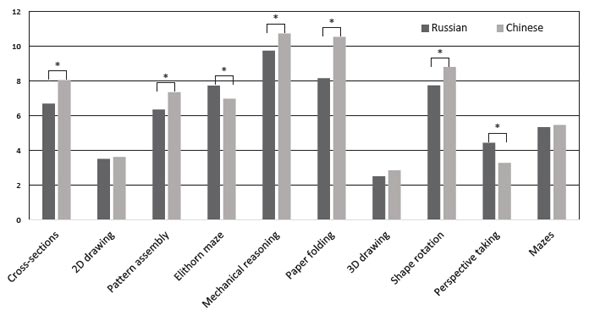
Figure 1. Mean comparisons for Chinese and Russian samples
Note. *=significant difference at .01 level.
Discussion
Our aims were: 1) to investigate the factorial structure of spatial abilities in Russian and Chinese samples; 2) to check whether our findings replicate the findings by Rimfeld and colleagues (2017); and 3) to explore the relative strengths and weaknesses in performance on the King’s challenge battery across the two samples.
Overall, our data showed somewhat different factor structure for the Russian and Chinese samples. In the Russian sample, the unifactorial structure for both selected (unpublished data) and unselected UK samples was replicated. In the Chinese sample, a second factor emerged. The Russian, Chinese, and unselected UK samples (see Fig. 2 in Rimfeld et al., 2017) showed very similar factor loadings, although the cross-sections and mechanical reasoning tests formed a separate factor in the Chinese sample. Several explanations may be proposed for the observed differences in the factorial structure.
The differences may be due to cultural and educational differences between the countries. These cultural differences may also explain the differences in average performance across the countries for these tests. Chinese students demonstrated higher scores for cross-sections and mechanical reasoning (8.06 and 10.75) than the Russian students (6.71 and 9.76).
The advantage in these skills by Chinese students might be partly explained by the features of the written Chinese language. It has previously been shown that both visual-orthographic processing and spatial analysis are essential for learning to read a Chinese character (Tan et al., 2005). Also, spatial ability was linked with writing in Chinese (Flaherty & Connolly, 1995). If this is the case, the cross-sections task may rely on an over-trained ability in the Chinese participants, as the task of retrieving part of the information from a unity (such as getting the shape of a section from a full figure) might be related to the need to compose a Chinese character out of several elements. It is possible that continuous engagement in such language processing leads to superior development of the relevant brain networks, which in turn leads to advantages in spatial ability and mathematics.
The mechanical reasoning test requires reading instructions for each item of the test, since the instructions differ from item to item. This might have led to the formation of separate “verbal” factor composed of these two tests. For other spatial ability tests in the battery, the instructions remained the same for all items. In addition, other tests, such as paper folding, do not rely on character-composing logic, as they do not involve operations with parts to compose a unity. Another test in the battery that may also rely on the ability to construct unity from several parts is pattern assembly. Therefore, this test can also be expected to rely on an underlying verbal component and to load on the verbal factor. In our study we did not observe this, which may be a result of the relatively small sample size.
Interestingly, pattern assembly (along with paper folding and 3D drawing) show relatively high loadings on the second factor (although not exceeding the level of .3 after rotation). This might suggest that these tests are not robustly loading on either of the factors. Furthermore, the loadings for perspective-taking were almost equal for the two factors, and did not exceed .3. Perspective taking is sometimes considered to be a large-scale test (Hegarty & Waller, 2004), and might have less links with other small-scale tests. This is also evident from its correlation coefficients with other tests in the battery in the Chinese sample (all correlations are less than .3). This pattern was not observed in the Russian sample.
The emergence of the second factor in the Chinese sample can be partly explained by the low split-half reliability for the mechanical reasoning test (.56 for the Russian and .54 for the Chinese samples). This may have led to error-related factor differences. Additional analyses on this test showed somewhat strange patterns of correlations between items within the test: some items correlated negatively with each other. This suggests low reliability for this test. Given that there was a time limit of 25 seconds for each item (and a need to read new instructions each time), participants with high spatial ability might have failed to give a correct answer in time, which might have led to the test having a reduced reliability.
To sum up, there could be indeed a second factor in spatial ability for the Chinese sample. The second factor might have emerged because the two tests (cross-sections and mechanical reasoning) are linked to verbal reasoning more than other tests. Further studies with more participants and other measures, e.g. verbal ability, are needed in order to improve our understanding of the SA factor structure in the Chinese population.
Our data also showed significant average differences in performance between the two samples. The Chinese students outperformed the Russian student on five out of 10 spatial tests (cross-sections, pattern assembly, mechanical reasoning, paper folding, and shape rotation). These results are consistent with previous research that demonstrated better average results by Chinese school children in mathematics and science (e.g., Programme for International Student assessment results; PISA; OECD, 2016). The mathematical advantage shown by children of all ages from Asian-Pacific countries has been very well established (Imbo & LeFevre, 2009; Mullis, Martin, & Foy, 2008). This advantage might continue to the university level and be reflected in spatial ability performance.
The observed average differences may also be related to the differences in the level of general intelligence and other relevant abilities between the two samples. The Chinese students were recruited from top-tier universities, where students are highly selected for admission based on their abilities (including mathematical reasoning). Although the Russian students were also recruited from top universities, the Russian selection criteria do not include such tests, but rather depend on the Unified State Exam performance, which varies for different majors/degrees.
Other reasons for the observed average differences may include school curricular differences. The lower general performance of the Russian participants can be related to the exclusion (since 2010) of technical drawing from the school National Curriculum. As a result, skills related to performance in some tests, such as cross-sections and mechanical reasoning, might have been under-trained in the students who participated in the current study. Moreover, in China, in contrast to Western countries, the abacus is still used to teach simple mathematical operations such as addition/subtraction. It has been shown that this leads to increased activation of the brain areas linked to spatial processing (Wu et al., 2009).
However, the Russian participants showed better performance in Elithorn maze and perspective-taking tasks than the Chinese participants. A possible explanation might be that some tests require greater flexibility (e.g., one needs to switch between different strategies to solve the task in the Elithorn maze), which was shown to be lower in Chinese population, in comparison with the Belgian and Canadian populations (Imbo & LeFevre, 2009).
Conclusion
Our data only partially replicated the findings of Rimfeld and colleagues (2017): while the unifactoral structure of spatial ability was replicated in the Russian sample, two factors emerged for the Chinese sample. The study also demonstrated some cross-cultural differences in spatial ability. More research is needed to replicate the pattern of relative strengths and weaknesses across the populations and to explore potential sources of these differences.
Limitations
One limitation of the present study was the relatively small size of the Chinese sample. In addition, some internet connection issues were reported by some participants, which led to a reduced dataset. The samples in the two countries were drawn from student populations from top universities in their countries. However, the selection criteria differed across the universities, and that could have led to differences across the samples in average intelligence and other relevant characteristics.
Acknowledgements
This work was supported by the Ministry of Education and Science of the Russian Federation within project No. 25.8566.2017/9.10
References
Aristova, I., Esipenko, E., Sharafieva, K., Maslennikova, E., Chipeeva, N., Feklicheva, I., … & Kovas, Y. (2018). Sovremennye podkhody v izuchenii prostranstvennykh sposobnostei: struktura i etiologia individualʹnykh razlichii [Modern approaches in the study of spatial abilities: a structure and etiology of individual differences]. Voprosy Psychologii [Issues of psychology], 1, 118-126.
Blajenkova, O., Motes, M.A., & Kozhevnikov, M. (2005). Individual differences in the representations of novel environments. Journal of Environmental Psychology, 25(1), 97-109. https://doi.org/10.1016/j.jenvp.2004.12.003
Carroll, J.B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge University Press. https://doi.org/10.1080/00140139508925174
Cerny, C.A. & Kaiser, H.F. (1977). A study of a measure of sampling adequacy for factor-analytic correlation matrices. Multivariate Behavioral Research, 12(1), 43-47. https://doi.org/10.1207/s15327906mbr1201_3
Comrey, A.L. & Lee, H.B. (1992). A first course in factor analysis (2nd ed.). Hillsdale, N.J., US: Lawrence Erlbaum Associates, Inc.
Coutrot, A., Silva, R., Manley, E., de Cothi, W., Sami, S., Bohbot, V., …& Hornberger, M. (2017). Planetary-wide organization of human cognition. bioRxiv, 188870. http://dx.doi.org/10.1101/188870
De Beni, R., Pazzaglia, F., & Gardini, S. (2006). The role of mental rotation and age in spatial perspective‐taking tasks: when age does not impair perspective‐taking performance. Applied cognitive psychology, 20(6), 807-821. https://doi.org/10.1002/acp.1229
Esipenko, E., Maslennikova, E., Budakova, A., Sharafieva, K., Ismatullina, V., Feklicheva, I., … & Kovas, Y. (2018) Spatial ability of male and female students completing humanities vs. technical degrees. Psychology in Russia: State of the Art, 11(4), 40-52. https://doi.org/10.11621/pir.2018.0403
Flaherty, M. & Connolly, M. (1995). Space perception, coordination and a knowledge of Kanji in Japanese and non-Japanese. Psychologia, 38, 229-237.
Gitterman, M.R. & Sies, L.F. (1992). Nonbiological determinants of the organization of language in the brain: A comment on Hu, Qiou and Zhong. Brain and Language, 43, 162-165. https://doi.org/10.1016/0093-934X(92)90027-C
Gogos, A., Gavrilescu, M., Davison, S., Searle, K., Adams, J., Rossell, S. L., ... & Egan, G.F. (2010). Greater superior than inferior parietal lobule activation with increasing rotation angle during mental rotation: an fMRI study. Neuropsychologia, 48(2), 529-535. https://doi.org/10.1016/j.neuropsychologia.2009.10.013
Hegarty, M. & Waller, D. (2004). A dissociation between mental rotation and perspective-taking spatial abilities. Intelligence, 32(2), 175-191. https://doi.org/10.1016/j.intell.2003.12.001
Hegarty, M., Montello, D.R., Richardson, A.E., Ishikawa, T., & Lovelace, K. (2006). Spatial abilities at different scales: Individual differences in aptitude-test performance and spatial-layout learning. Intelligence, 34(2), 151-176. https://doi.org/10.1016/j.intell.2005.09.005
Hugdahl, K., Thomsen, T., & Ersland, L. (2006). Sex differences in visuo-spatial processing: an fMRI study of mental rotation. Neuropsychologia, 44(9), 1575-1583. https://doi.org/10.1016/j.neuropsychologia.2006.01.026
Imbo, I. & LeFevre, J.A. (2010). The role of phonological and visual working memory in complex arithmetic for Chinese-and Canadian-educated adults. Memory & Cognition, 38(2), 176-185. https://doi.org/10.3758/MC.38.2.176
Jansen, P (2009). The dissociation of small- and large-scale spatial abilities in school-age children. Perceptual and Motor Skills, 109(2), 357-61. https://doi.org/10.2466/PMS.109.2.357-361
Jansen, P., Schmelter, A., & Heil, M. (2010). Spatial knowledge acquisition in younger and elderly adults: A study in a virtual environment. Experimental Psychology, 57(1), 54. https://doi.org/10.1027/1618-3169/a000007
Jansen, P., Wiedenbauer, G., & Hahn, N. (2010). Manual rotation training improves direction-estimations in a virtual environmental space. European Journal of Cognitive Psychology, 22(1), 6-17. http://dx.doi.org/10.1080/09541440802678487
Kell, H., Lubinski, D., Benbow, C., & Steiger, J. (2013). Creativity and technical innovation: spatial ability's unique role. Psychol Sci. 24(9), 1831-1836. https://doi.org/10.1177/0956797613478615
Kosslyn, S.M. & Thompson, W.L. (2003). When is early visual cortex activated during visual mental imagery? Psychological bulletin, 129(5), 723. https://doi.org/10.1037/0033-2909.129.5.723
Kozhevnikov, M. & Hegarty, M. (2001). A dissociation between object manipulation spatial ability and spatial orientation ability. Memory & Cognition, 29(5), 745-756. https://doi.org/10.1016/j.intell.2003.12.001
Kozhevnikov, M., Motes, M.A., Rasch, B., & Blajenkova, O. (2006). Perspective‐taking vs. mental rotation transformations and how they predict spatial navigation performance. Applied Cognitive Psychology, 20(3), 397-417. https://doi.org/10.1002/acp.1192
Lohman, D.F. (1979). Spatial Ability: A Review and Reanalysis of the Correlational Literature (No. TR-8). Stanford, California: Stanford University School of Education
Lohman, D.F., Pellegrino. J.W., Alderton, D.L., & Regian, J.W. (1987). Dimensions and components of individual differences in spatial abilities. In S.H. Irvin & S.E. Newstead (Eds.), Intelligence and Cognition: Contemporary frames of reference. Boston: Martinus Nijhoff.
Lohman, D.F. (1996). Spatial ability and g. In I. Dennis & P. Tapsfield (Eds.), Human abilities: Their nature and measurement (pp. 97-116).
Lohman, D.F. & Nichols, P.D. (1990). Training spatial abilities: Effects of practice on rotation and synthesis tasks. Learning and Individual Differences, 2(1), 67-93.
McGee, M.G. (1979). Human spatial abilities: Psychometric studies and environmental, genetic, hormonal, and neurological influences. Psychological bulletin, 86(5), 889.
Morris, R.G. & Parslow, D.M. (2004). Neurocognitive components of spatial memory. In G. Allen (Ed.), Human Spatial Memory: Remembering where (pp. 217–247). Lawrence Erlbaum Associates, Mahwah
Mullis, I., Martin, M.O., & Foy, P. (2008). TIMSS 2007 International Mathematics Report: Findings from IEA's Trends in International Mathematics and Science Study at the Eighth and Fourth Grades. Retrieved from https://timssandpirls.bc.edu/TIMSS2007/mathreport.html
OECD (2016), PISA 2015 Results (Volume I): Excellence and Equity in Education, PISA, OECD Publishing, Paris. Retrieved from http://dx.doi.org/10.1787/9789264266490-en
Parslow, D.M., Rose, D., Brooks, B., Fleminger, S., Gray, J.A., Giampietro, V., … & Morris, R.G. (2004). Allocentric spatial memory activation of the hippocampal formation measured with fMRI. Neuropsychology, 18(3), 450-61. https://doi.org/10.1037/0894-4105.18.3.450
Revelle, W. & Rocklin, T. (1979). Very simple structure: An alternative procedure for estimating the optimal number of interpretable factors. Multivariate Behavioral Research, 14(4), 403-414. https://doi.org/10.1207/s15327906mbr1404_2
Rimfeld, K., Shakeshaft, N.G., Malanchini, M., Rodic, M., Selzam, S., Schofield, K., ... & Plomin, R. (2017). Phenotypic and genetic evidence for a unifactorial structure of spatial abilities. Proceedings of the National Academy of Sciences, 114(10), 2777-2782. https://doi.org/10.1073/pnas.1607883114
Rodic, M., Tikhomirova. T., Kolienko, T., Malykh, S., Bogdanova, O., Zueva, D.Y., … & Kovas, Y. (2015) Spatial complexity of character based writing systems and arithmetic in primary school: a longitudinal study. Front. Psychol. 6:333. https://doi.org/10.3389/fpsyg.2015.00333
Sakamoto, M. & Spiers, M.V. (2014). Sex and cultural differences in spatial performance between Japanese and North Americans. Archives of sexual behavior, 43(3), 483-491. https://doi.org/10.1007/s10508-013-0232-8
Shakeshaft, N.G., Rimfeld, K., Schofield, K.L., Selzam, S., Malanchini, M., Rodic, M., ... & Plomin, R. (2016). Rotation is visualization, 3D is 2D: using a novel measure to investigate the genetics of spatial ability. Scientific reports, 6. https://dx.doi.org/10.1038%2Fsrep30545
Shen, C., Vasilyeva, M., & Laski, E.V. (2016). Here, but not there: Cross-national variability of gender effects in arithmetic. Journal of experimental child psychology, 146, 50-65. https://doi.org/10.1016/j.jecp.2016.01.016
Shepard, R.N. & Metzler, J. (1971). Mental rotation of three-dimensional objects. Science, 171(3972), 701-703. https://doi.org/10.1126/science.171.3972.701
State Federal Educational standard for school (2010, November 11). Retrieved from https://xn--80abucjiibhv9a.xn--p1ai/%D0%B4%D0%BE%D0%BA%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D1%8B/938
Tan, L.H., Spinks, J.A., Eden, G., Perfetti, C.A., & Siok, W.T. (2005). Reading depends on writing, in Chinese. Proc. Natl. Acad. Sci. U.S.A. 102 8781–8785 https://doi.org/10.1073/pnas.0503523102
Toivainen, T., Pannini, G., Papageorgiou, K.A., Malanchini, M., Rimfeld, K., Shakeshaft, N., & Kovas, Y. (2018). Prenatal testosterone does not explain sex differences in spatial ability. Sci Rep., 8(1), 13653. https://doi.org/10.1038/s41598-018-31704-y
Tosto, M.G., Hanscombe, K.B., Haworth, C.M., Davis, O.S., Petrill, S.A., Dale, P.S., & Kovas, Y. (2014). Why do spatial abilities predict mathematical performance? Developmental science, 17(3), 462-470. https://dx.doi.org/10.1111%2Fdesc.12138
Uttal, D.H., Meadow, N.G., Tipton, E., Hand, L.L., Alden, A.R.,Warren, C., & Newcombe, N.S. The malleability of spatial skills: a meta-analysis of training studies. Psychol Bull.139(2):352-402. doi: 10.1037/a0028446. Epub 2012 Jun 4. https://doi.org/10.1037/a0028446
Wang, Y. (2014). Unveiling the Cognitive Mechanisms of Eyes: The Visual Sensor Vs. the Perceptive Browser of the Brain. International Journal of Cognitive Informatics and Natural Intelligence (IJCINI), 8(1), 36-50. https://doi.org/10.4018/ijcini.2014010103
Wang, L., Cohen, A., & Carr, M. (2014). Spatial Ability at Two Scales of Representation: A Meta-Analysis. Learning and Individual Differences, 36(1), 140-144. https://doi.org/10.1016/j.lindif.2014.10.006
Wu, T.H., Chen, C.L., Huang, Y.H., Liu, R.S., Hsieh, J.C., & Lee, J.J. (2009). Effects of long-term practice and task complexity on brain activities when performing abacus-based mental calculations: a PET study. Eur. J. Nucl. Med. Mol. Imaging 36, 436-445. https://doi.org/10.1007/s00259-008-0949-0
Zacks, J.M., Mires, J., Tversky, B., & Hazeltine, E. (2000). Mental spatial transformations of objects and perspective. Spatial Cognition and Computation, 2(4), 315-332. https://doi.org/10.1023/A:1015584100204
Appendix
Table 1
Correlations for King’s Challenge (KC) tests (Russia)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1. Cross-sections |
- |
|
|
|
|
|
|
|
|
|
|
2. 2D drawing |
.47 |
- |
|
|
|
|
|
|
|
|
|
3. Pattern assembly |
.38 |
.41 |
- |
|
|
|
|
|
|
|
|
4. Elithorn maze |
.27 |
.34 |
.22 |
- |
|
|
|
|
|
|
|
5. Mechanical reasoning |
.46 |
.45 |
.35 |
.31 |
- |
|
|
|
|
|
|
6. Paper folding |
.49 |
.49 |
.39 |
.30 |
.46 |
- |
|
|
|
|
|
7. 3D drawing |
.47 |
.60 |
.39 |
.32 |
.48 |
.55 |
- |
|
|
|
|
8. Shape rotation |
.41 |
.47 |
.39 |
.25 |
.42 |
.49 |
.49 |
- |
|
|
|
9. Perspective taking |
.34 |
.40 |
.29 |
.25 |
.34 |
.38 |
.46 |
.39 |
- |
|
|
10. Mazes |
.29 |
.35 |
.34 |
.26 |
.35 |
.36 |
.38 |
.34 |
.27 |
- |
|
11. Total score |
.70 |
.69 |
.62 |
.48 |
.68 |
.77 |
.74 |
.73 |
.65 |
.55 |
Note. All correlations were significant after Bonferroni correction (p<0.001)
Table 2
Correlations for King’s Challenge (KC) tests (China)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1.Cross-sections |
|
|
|
|
|
|
|
|
|
|
|
2. 2D drawing |
.32** |
|
|
|
|
|
|
|
|
|
|
3. Pattern assembly |
.36** |
.32** |
|
|
|
|
|
|
|
|
|
4. Elithorn maze |
.28** |
.41** |
.32** |
|
|
|
|
|
|
|
|
5. Mechanical reasoning |
.45** |
.30** |
.29** |
.22** |
|
|
|
|
|
|
|
6. Paper folding |
.43** |
.59** |
.34** |
.39** |
.42** |
|
|
|
|
|
|
7. 3D drawing |
.40** |
.52** |
.35** |
.36** |
.40** |
.52** |
|
|
|
|
|
8. Shape rotation |
.27** |
.36** |
.39** |
.47** |
.25** |
.45** |
.46** |
|
|
|
|
9. Perspective taking |
.23** |
.25** |
.20** |
.17* |
.18* |
.25** |
.24** |
.27** |
|
|
|
10.Mazes |
.16* |
.30** |
.22** |
.31** |
.15* |
.36** |
.36** |
.36** |
.15* |
|
|
11. Total score |
.70** |
.70** |
.60** |
.60** |
.70** |
.80** |
.68** |
.70** |
.51** |
.58** |
Note. ** Correlation is significant at the 0.01 level (2-tailed) after Bonferroni correction, * Correlation is significant at the 0.05 level (2-tailed) after Bonferroni correction.
Table 3
Communalities for Russian and Chinese sample
|
|
Russian |
Chinese |
|
Cross-sections |
.483 |
.637 |
|
2D drawing |
.578 |
.504 |
|
Pattern assembly |
.372 |
.218 |
|
Elithorn maze |
.262 |
.484 |
|
Mechanical reasoning |
.502 |
.584 |
|
Paper folding |
.547 |
.580 |
|
3D drawing |
.621 |
.436 |
|
Shape rotation |
.492 |
.574 |
|
Perspective taking |
.395 |
.096 |
|
Mazes |
.342 |
.430 |
Table 4.
Mean comparison (t-stat counted as Russian sample vs. Chinese)
|
|
N (Ch) |
Mean (Ch) |
SD (Ch) |
N (Rus) |
M (Rus) |
SD (Rus) |
t-stat |
d Cohen |
adjusted p-value |
|
Cross-sections |
229 |
8.06 |
3.74 |
922 |
6.71 |
3.65 |
-4.89 |
0.37 |
.00 |
|
2D drawing |
229 |
3.63 |
1.19 |
918 |
3.53 |
1.23 |
-1.19 |
0.09 |
1.00 |
|
Pattern assembly |
229 |
7.37 |
3.10 |
909 |
6.37 |
3.04 |
-4.40 |
0.33 |
.00 |
|
Elithorn maze |
227 |
6.99 |
2.15 |
904 |
7.74 |
1.97 |
4.79 |
0.37 |
.00 |
|
Mechanical reasoning |
225 |
10.75 |
2.43 |
902 |
9.76 |
2.70 |
-5.37 |
0.38 |
.00 |
|
Paper folding |
224 |
10.55 |
3.54 |
897 |
8.17 |
4.25 |
-8.63 |
0.58 |
.00 |
|
3D drawing |
224 |
2.87 |
1.80 |
889 |
2.52 |
1.82 |
-2.60 |
0.19 |
.15 |
|
Shape rotation |
223 |
8.82 |
3.71 |
886 |
7.76 |
4.05 |
-3.74 |
0.27 |
.00 |
|
Perspective taking |
223 |
3.29 |
3.07 |
885 |
4.45 |
4.14 |
4.70 |
0.30 |
.00 |
|
Mazes |
222 |
5.47 |
2.06 |
883 |
5.35 |
2.03 |
-0.78 |
0.06 |
1.00 |
|
Total |
222 |
68.24 |
17.94 |
883 |
62.40 |
19.66 |
-4.26 |
0.30 |
.00 |
Note: significant differences between samples are in bold
Figure 1. Density plot distributions for all tests (Russian sample)
Figure 2. Density plot distributions for all tests (Chinese sample)
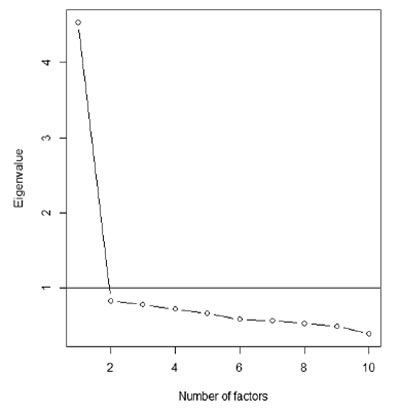
Figure 3. Screeplot for PCA on KC subtests for Russian sample
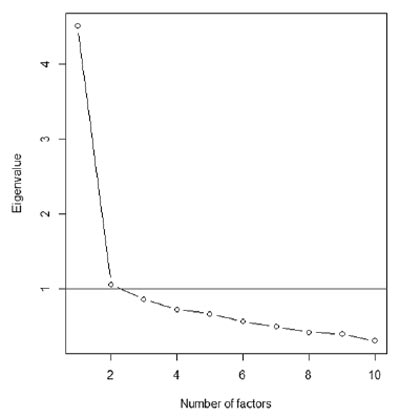
Figure 4. Screeplot for PCA on KC subtests for Russian sample
To cite this article: Likhanov M. V. et al. (2018). The Factorial Structure of Spatial Abilities in Russian and Chinese Students. Psychology in Russia: State of the Art, 11 (4), 96-114.
The journal content is licensed with CC BY-NC “Attribution-NonCommercial” Creative Commons license.










